基于图论的变换器冗余开关自动识别方法

莫李平; 宋吉祥; 陈桂鹏

doi:10.13700/j.bh.1001-5965.2023.0358

基于图论的变换器冗余开关自动识别方法

doi: 10.13700/j.bh.1001-5965.2023.0358

莫李平^{1, 2},
宋吉祥^{1, 2},
陈桂鹏^{1, 2, ,}

1.
厦门大学深圳研究院，深圳 518000
2.
厦门大学航空航天学院，厦门 361000

基金项目:

广东省基础与应用基础研究基金(2022A1515011616)；中央高校基本科研业务费专项资金(20720220083)

详细信息

通讯作者:
E-mail：cgp2017@xmu.edu.cn

中图分类号: TM46；O157.5
计量
- 文章访问数: 143
- HTML全文浏览量: 26
- PDF下载量: 18
- 被引次数: 0
出版历程
- 收稿日期: 2023-06-14
- 录用日期: 2023-10-11
- 网络出版日期: 2024-01-23
- 整期出版日期: 2025-05-31

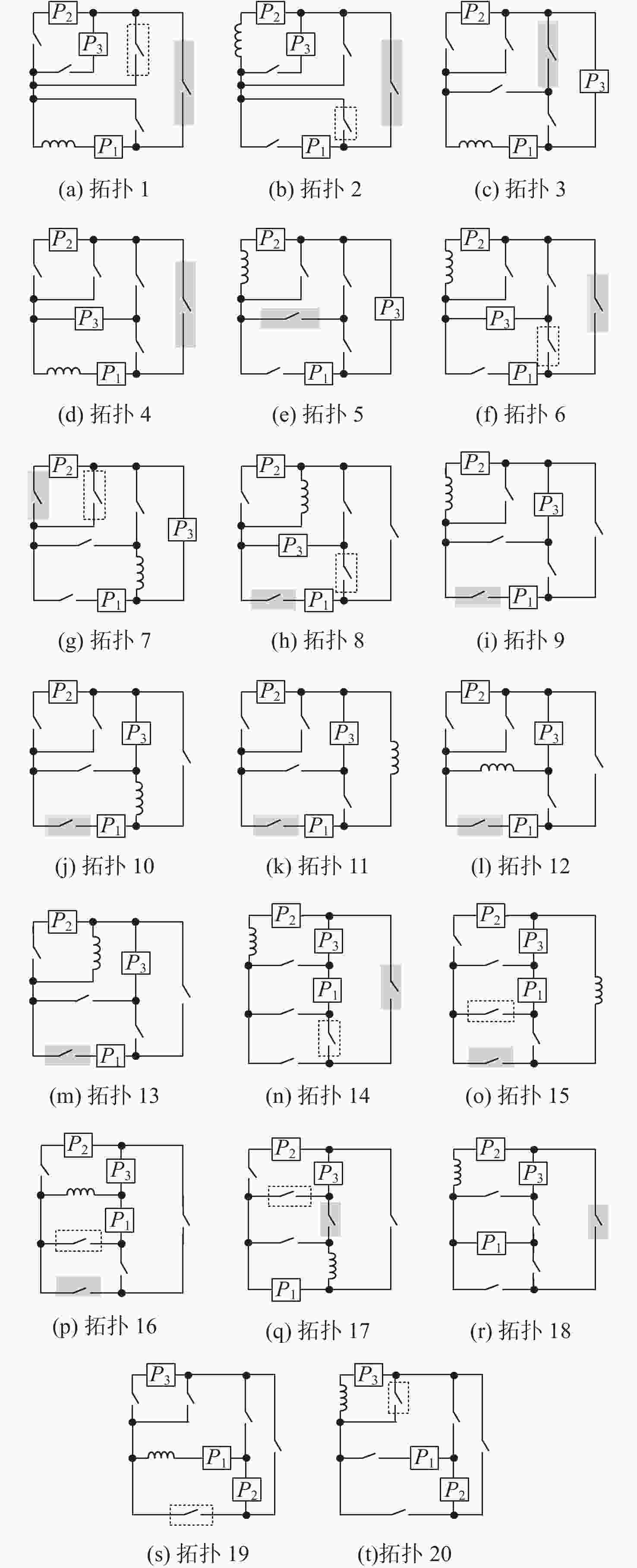
Auto identification method for redundant switches in converters based on graph theory

MO Liping^{1, 2},
SONG Jixiang^{1, 2},
CHEN Guipeng^{1, 2
, ,}

1.
Shenzhen Research Institute of Xiamen University，Shenzhen 518000，China
2.
School of Aerospace Engineering，Xiamen University，Xiamen 361000，China

Funds:

Guangdong Basic and Applied Basic Research Foundation (2022A1515011616); The Fundamental Research Funds for the Central Universities (20720220083)

More Information

Corresponding author: E-mail：cgp2017@xmu.edu.cn

摘要

摘要:
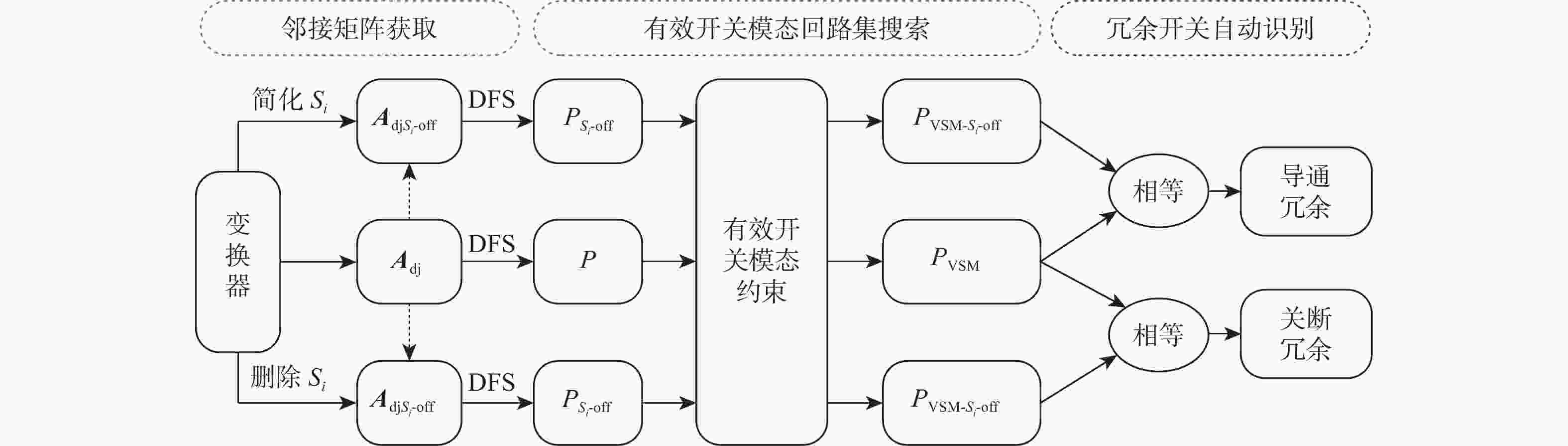
电能变换需求日益增长，推演具有不同性能的新型变换器成为研究热点。当前的推演方法大多未考虑变换器开关冗余的因素，导致推演结果中同时存在含冗余开关的变换器和不含冗余开关的变换器。为从海量的推演结果中快速剔除含冗余开关的变换器，开展了变换器冗余开关自动识别研究。分析变换器冗余开关与其有效开关模态的关系，并在此基础上归纳冗余开关的识别准则；基于图论将识别准则转化为对应的图准则；应用图搜索算法结合图准则建立冗余开关自动识别方法。为验证冗余开关自动识别方法的可行性，将其用于识别现存单电感多端口变换器的冗余开关，识别结果表明：所提方法可以批量、准确地识别出变换器的所有冗余开关，验证了方法的可行性。
- 图论 /
- 变换器 /
- 冗余开关 /
- 自动识别 /
- 开关模态
Abstract:
Up to now, massive power electronics converters have been derived to satisfy various demands in practical applications. However, most of these methods focus on discovering effective converters, ignoring the redundant switches in converters. This paper aims to delete converters with redundant switches efficiently. First, the identification principle is introduced based on the connection between legitimate switching modes and redundant switches. After that, the principle is transformed into the corresponding graph principle. Finally, graph theory and graph searching algorithms are used to develop the auto identification method based on the graph principle. The results demonstrate that all redundant switches may be effectively recognized with the use of computers when the suggested method is applied to single-inductor multi-port converters.
- graph theory /
- converters /
- redundant switches /
- auto identification /
- switching modes

HTML全文

图 1 导通冗余开关简化前后变换器的有效开关模态种类

Figure 1. Valid switching modes types of converters before and after turn-on redundant switches are simplified

下载: 全尺寸图片幻灯片

图 2 关断冗余开关删除前后变换器的有效开关模态种类

Figure 2. Valid switching modes types of converters before and after turn-off redundant switches are deleted

下载: 全尺寸图片幻灯片

图 3 冗余开关自动识别总体流程

Figure 3. Main flowchart of auto identification of redundant switches

下载: 全尺寸图片幻灯片

图 4 原变换器邻接矩阵及简化开关S₁和删除开关S₁后的邻接矩阵

Figure 4. Adjacent matrix of original converter and adjacent matrices of converters after switch S₁ are simplified or deleted

下载: 全尺寸图片幻灯片

图 5 电路正常工作的基本原理

Figure 5. Fundamental principles of workable circuits

下载: 全尺寸图片幻灯片

图 6 基本原理1对应的4种无效开关模态

Figure 6. Four kinds of invalid switching modes based on fundamental principles of workable circuits 1

下载: 全尺寸图片幻灯片

图 7 有效开关模态回路集获取流程

Figure 7. Flowchart of obtaining loop set of valid switching modes

下载: 全尺寸图片幻灯片

图 8 自动识别出的20个含冗余开关的单电感多端口变换器

Figure 8. 20 automatically identified single-inductor multi-port converters with redundant switches

下载: 全尺寸图片幻灯片

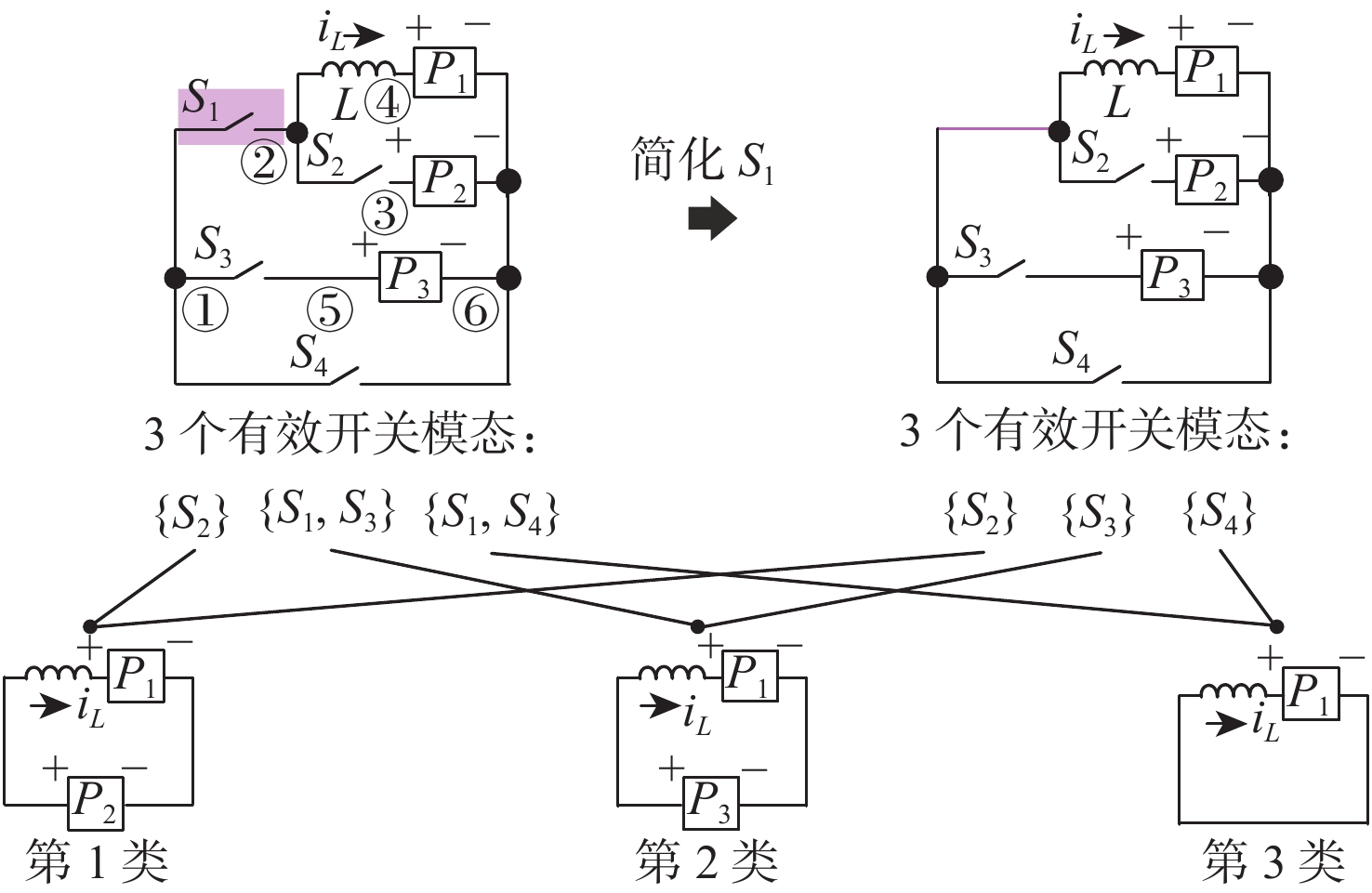
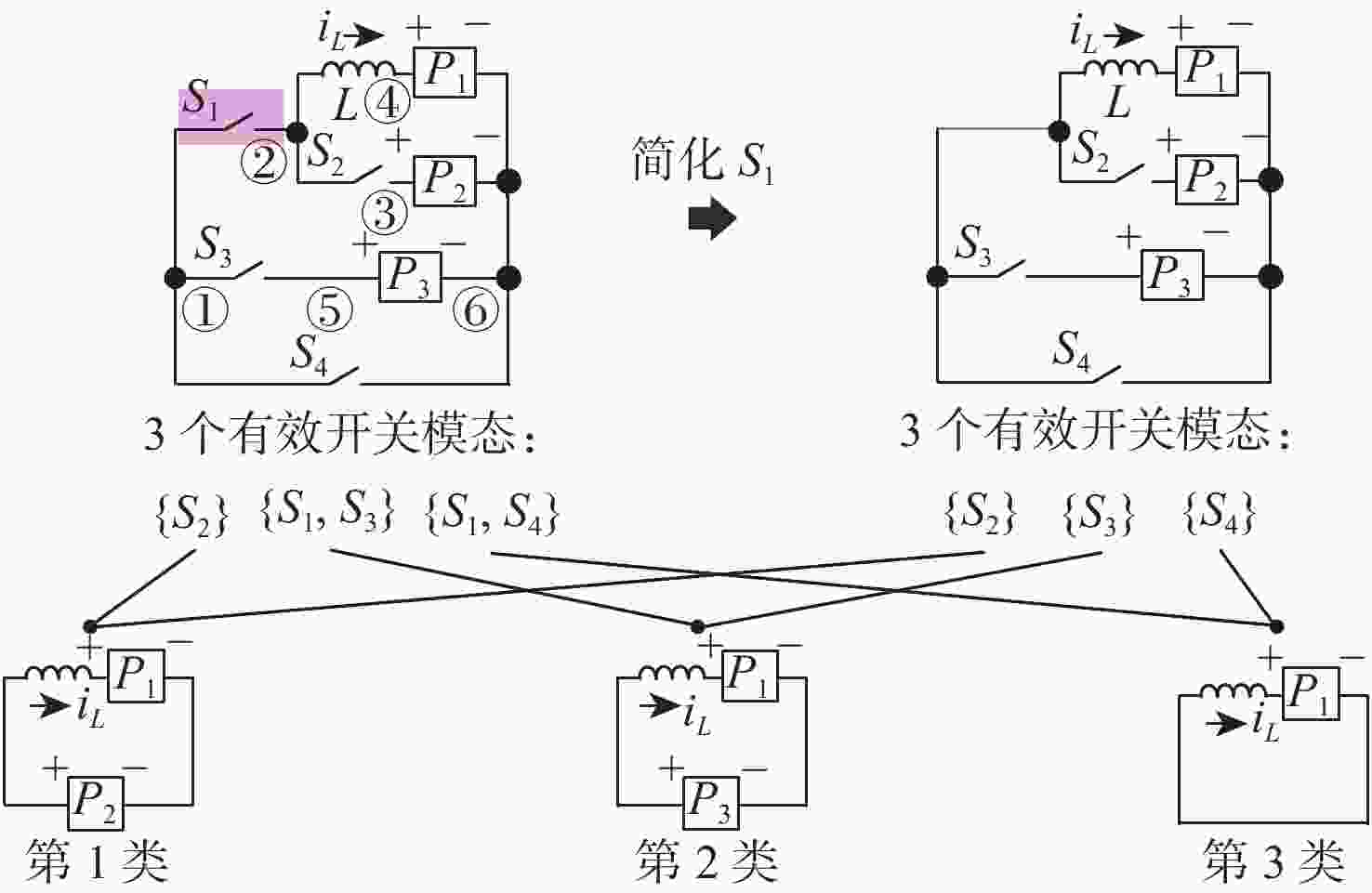
表 1 图1变换器的导通冗余开关识别结果

Table 1. Identification results of turn-on redundant switch for converter in Fig. 1

变化器简图	有效开关模态	回路集与识别结果
原变换器	v_sm1={S₂} v_sm2={S₁, S₃} v_sm3={S₁, S₄}	$ \begin{gathered} {{{P}}_{{\mathrm{VSM}}}} = \left\{ {p_{{\mathrm{vsm}}1}} = (L,{P_{1 {\text{-}} {\rm{pn}}}},{P_{2 {\text{-}} {\rm{np}}}}),\right. \\ \qquad{p_{{\mathrm{vsm}}2}} = (L,{P_{1 {\text{-}} {\rm{pn}}}},{P_{3 {\text{-}} {\rm{np}}}}), {p_{{\mathrm{vsm}}3}} = \\ \qquad \left.(L,{P_{1 {\text{-}} {\rm{pn}}}})\right\} \\ \end{gathered} $
简化S₁	v_sm1={S₂} v_sm2={S₃} v_sm3={S₄}	$\begin{gathered} {{{P}}_{{\mathrm{VSM}} {\text{-}} {{S}}_1 {\text{-}} {\mathrm{on}}}} = \left\{ {p_{{\rm{vsm}}1}} = (L,{P_{1 {\text{-}} {\rm{pn}}}},{P_{2 {\text{-}} {\rm{np}}}}),\right. \\ \qquad {p_{{\rm{vsm}}2}} = (L,{P_{1 {\text{-}} {\rm{pn}}}},{P_{3 {\text{-}} {\rm{np}}}}), {p_{{\rm{vsm}}3}} = \\ \qquad \left. (L,{P_{1 {\text{-}} {\rm{pn}}}}) \right\} \\ \end{gathered}$ P_VMS=${{{P}}_{{\mathrm{VSM}} {\text{-}} {{S}}_1 {\text{-}} {\mathrm{on}}}} $，S₁导通冗余
简化S₂	v_sm1={S₁} v_sm2={S₃} v_sm3={S₄}	$\begin{gathered} {{{P}}_{{\mathrm{VSM}} {\text{-}} {{S}}_2 {\text{-}} {\mathrm{on}}}} = \left\{ {p_{{\rm{vsm}}1}} = (L,{P_{1 {\text{-}} {\rm{pn}}}},{P_{2 {\text{-}} {\rm{np}}}}), \right. \\ \qquad {p_{{\rm{vsm}}2}} = (L,{P_{1 {\text{-}} {\rm{pn}}}},{P_{2 {\text{-}} {\rm{np}}}}), {p_{{\rm{vsm}}3}} = \\ \qquad \left. (L,{P_{1 {\text{-}} {\rm{pn}}}},{P_{2 {\text{-}} {\rm{np}}}}) \right\} \\ \end{gathered} $ P_VMS≠${{{P}}_{{\mathrm{VSM}} {\text{-}} {{S}}_2 {\text{-}} {\mathrm{on}}}} $，S₂不是导通冗余
简化S₃	v_sm1={S₁} v_sm2={S₂}	$\begin{gathered} {{{P}}_{{\mathrm{VSM}} {\text{-}} {{S}}_3 {\text{-}} {\mathrm{on}}}} = \left\{ {p_{{\rm{vsm}}1}} = (L,{P_{1 {\text{-}} {\rm{pn}}}},{P_{3 {\text{-}} {\rm{np}}}}), \right. \\ \left.{p_{{\rm{vsm}}2}} = (L,{P_{1 {\text{-}} {\rm{pn}}}},{P_{2 {\text{-}} {\rm{np}}}}) \right\} \end{gathered} $ P_VSM≠${{{P}}_{{\mathrm{VSM}} {\text{-}} {{S}}_3 {\text{-}} {\mathrm{on}}}} $，S₃不是导通冗余
简化S₄	v_sm1={S₁} v_sm2={S₂}	$ \begin{gathered} {{{P}}_{{\mathrm{VSM}} {\text{-}} {{S}}_4 {\text{-}} {\mathrm{on}}}} = \left\{ {p_{{\rm{vsm}}1}} = (L,{P_{1 {\text{-}} {\rm{pn}}}}),\right. \\ \left.{p_{{\rm{vsm}}2}} = (L,{P_{1 {\text{-}} {\rm{pn}}}},{P_{2 {\text{-}} {\rm{np}}}}) \right\} \end{gathered} $ P_VMS≠${{{P}}_{{\mathrm{VSM}} {\text{-}} {{S}}_4 {\text{-}} {\mathrm{on}}}} $，S₄不是导通冗余

下载: 导出CSV

表 2 图2变换器的关断冗余开关识别结果

Table 2. Identification results of turn-off redundant switch for converter in Fig. 2

变化器简图	有效开关模态	回路集与识别结果
原变换器	v_sm1={S₁} v_sm2={S₂, S₃} v_sm3={S₂, S₅} v_sm4={S₃, S₄}	$ \begin{gathered} {{{P}}}_{{\mathrm{VSM}}}= \left\{{p}_{{\rm{vsm}}1}=(L,{P}_{3{\text{-}} {\rm{pn}}}),\right. \\ \qquad {p}_{{\rm{vsm}}2}=(L,{P}_{3{\text{-}} {\rm{pn}}},{P}_{1{\text{-}} {\rm{np}}}), \\ \qquad {p}_{{\rm{vsm}}3}=(L,{P}_{3{\text{-}} {\rm{pn}}},{P}_{2{\text{-}} {\rm{pn}}}, {P}_{1{\text{-}} {\rm{np}}}), \\ \qquad \left.{p}_{{\rm{vsm}}4}=(L,{P}_{3{\text{-}} {\rm{pn}}},{P}_{2{\text{-}} {\rm{np}}})\right\} \\ \end{gathered} $
删除S₁	v_sm1={S₄, S₅} v_sm2={S₂, S₃} v_sm3={S₂, S₅} v_sm4={S₃, S₄}	$ \begin{gathered} {{{P}}}_{{\mathrm{VSM}}{\text{-}}{{S}}_1{\text{-}}{\mathrm{off}}}= \left\{{p}_{{\rm{vsm}}1}=(L,{P}_{3{\text{-}} {\rm{pn}}}),\right. \\ \qquad {p}_{{\rm{vsm}}2}=(L,{P}_{3{\text{-}} {\rm{pn}}},{P}_{1{\text{-}} {\rm{np}}}), \\ \qquad {p}_{{\rm{vsm}}3}=(L,{P}_{3{\text{-}} {\rm{pn}}},{P}_{2{\text{-}} {\rm{pn}}}, {P}_{1{\text{-}} {\rm{np}}}), \\ \qquad \left.{p}_{{\rm{vsm}}4}=(L,{P}_{3{\text{-}} {\rm{pn}}},{P}_{2{\text{-}} {\rm{np}}})\right\} \\ \end{gathered} $ P_VSM=${{{P}}}_{{\mathrm{VSM}}{\text{-}}{{S}}_1{\text{-}}{\mathrm{off}}} $，S₁关断冗余
删除S₂	v_sm1={S₁} v_sm2={S₃, S₄}	$ \begin{gathered} {{{P}}_{{\mathrm{VSM}} {\text{-}} {{S}}_2 {\text{-}} {\mathrm{off}}}} = \left\{ {p_{{\rm{vsm}}1}} = (L,{P_{3 {\text{-}} {\rm{pn}}}}),\right. \\ \qquad \left.{p_{{\rm{vsm}}2}} = (L,{P_{3 {\text{-}} {\rm{pn}}}},{P_{2 {\text{-}} {\rm{np}}}}) \right\} \\ \end{gathered} $ P_VSM≠$ {{{P}}_{{\mathrm{VSM}} {\text{-}} {{S}}_2 {\text{-}} {\mathrm{off}}}} $，S₂不是关断冗余
删除S₃	v_sm1={S₁} v_sm2={S₂, S₅}	$ \begin{gathered} {{{P}}}_{{\mathrm{VSM}}{\text{-}}{{S}}_3{\text{-}}{\mathrm{off}}}= \left\{{p}_{{\rm{vsm}}1}=(L,{P}_{3{\text{-}} {\rm{pn}}}),\right. \\ \qquad \left.{p}_{{\rm{vsm}}2}=(L,{P}_{3{\text{-}} {\rm{pn}}},{P}_{2{\text{-}} {\rm{pn}}}, {P}_{1{\text{-}} {\rm{np}}})\right\} \\ \end{gathered} $ P_VSM≠${{{P}}}_{{\mathrm{VSM}}{\text{-}}{{S}}_3{\text{-}}{\mathrm{off}}} $，S₃不是关断冗余
删除S₄	v_sm1={S₁} v_sm2={S₂, S₃} v_sm3={S₂, S₅}	$ \begin{gathered}{{{P}}}_{{\mathrm{VSM}}{\text{-}}{{S}}_4{\text{-}}{\mathrm{off}}}= \left\{{p}_{{\rm{vsm}}1}=(L,{P}_{3{\text{-}} {\rm{pn}}}),\right. \\ \qquad {p}_{{\rm{vsm}}2}=(L,{P}_{3{\text{-}} {\rm{pn}}},{P}_{1{\text{-}} {\rm{np}}}), \\ \qquad \left.{p}_{{\rm{vsm}}3}=(L,{P}_{3{\text{-}} {\rm{pn}}},{P}_{2{\text{-}} {\rm{pn}}},\right. \\ \qquad \left. {P}_{1{\text{-}} {\rm{np}}})\right\} \\ \end{gathered} $ P_VSM≠${{{P}}}_{{\mathrm{VSM}}{\text{-}}{{S}}_4{\text{-}}{\mathrm{off}}} $，S₄不是关断冗余
删除S₅	v_sm1={S₁} v_sm2={S₂, S₃} v_sm3={S₃, S₄}	$ \begin{gathered}{{{P}}_{{\mathrm{VSM}} {\text{-}} {{S}}_5 {\text{-}} {\mathrm{off}}}} = \left\{ {p_{{\rm{vsm}}1}} = (L,{P_{3 {\text{-}} {\rm{pn}}}}),\right. \\ \qquad {p_{{\rm{vsm}}2}} = (L,{P_{3 {\text{-}} {\rm{pn}}}},{P_{1 {\text{-}} {\rm{np}}}}), \\ \qquad \left.{p_{{\rm{vsm}}2}} = (L,{P_{3 {\text{-}} {\rm{pn}}}},{P_{2 {\text{-}} {\rm{np}}}}) \right\} \\ \end{gathered} $ P_VSM≠${{{P}}_{{\mathrm{VSM}} {\text{-}} {{S}}_5 {\text{-}} {\mathrm{off}}}} $，S₅不是关断冗余

下载: 导出CSV

参考文献(20)

[1]	TANG Z T, YANG Y H, BLAABJERG F. Power electronics: the enabling technology for renewable energy integration[J]. CSEE Journal of Power and Energy Systems, 2022, 8(1): 39-52.
[2]	EHSANI M, SINGH K V, BANSAL H O, et al. State of the art and trends in electric and hybrid electric vehicles[J]. Proceedings of the IEEE, 2021, 109(6): 967-984. doi: 10.1109/JPROC.2021.3072788
[3]	PENG W Y, DU S J. The advances in conversion techniques in triboelectric energy harvesting: a review[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2023, 70(7): 3049-3062. doi: 10.1109/TCSI.2023.3261780
[4]	KIM J S, YOON J O, CHOI B D. A high-light-load-efficiency low-ripple-voltage PFM buck converter for IoT applications[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 5763-5772. doi: 10.1109/TPEL.2021.3131594
[5]	CHENG K W E, YE Y M. Duality approach to the study of switched-inductor power converters and its higher-order variations[J]. IET Power Electronics, 2015, 8(4): 489-496. doi: 10.1049/iet-pel.2014.0689
[6]	GNANASAMBANDAM K, RATHORE A K, EDPUGANTI A, et al. Current-fed multilevel converters: an overview of circuit topologies, modulation techniques, and applications[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3382-3401. doi: 10.1109/TPEL.2016.2585576
[7]	胡雪峰, 王琳, 代国瑞, 等. 单开关高增益Boost-Sepic集成变换器[J]. 中国电机工程学报, 2015, 35(8): 2018-2025. HU X F, WANG L, DAI G R, et al. High step-up Boost-Sepic integrated converters with a single switch[J]. Proceedings of the CSEE, 2015, 35(8): 2018-2025(in Chinese).
[8]	荣德生, 孙瑄瑨. 高增益耦合电感组合Buck-Boost-Zeta变换器[J]. 中国电机工程学报, 2020, 40(14): 4590-4601. RONG D S, SUN X J. High gain coupled inductance combination Buck-Boost-Zeta converter[J]. Proceedings of the CSEE, 2020, 40(14): 4590-4601(in Chinese).
[9]	DE ANDRADE J M, SALVADOR M A, COELHO R F, et al. General method for synthesizing high gain step-up DC-DC converters based on differential connections[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 13239-13254. doi: 10.1109/TPEL.2020.2996501
[10]	MO L P, CHEN G P, HUANG J M. From components to converters: a fundamental topology derivation method for single-inductor multi-input multi-output converters based on graph theory[C]// Proceedings of the IEEE International Conference on Power Electronics, Computer Applications. Piscataway: IEEE Press, 2021: 458-463.
[11]	DONG M, LIANG R J, YANG J, et al. Topology derivation of multiport DC-DC converters based on reinforcement learning[J]. IEEE Transactions on Power Electronics, 2023, 38(4): 5055-5064. doi: 10.1109/TPEL.2023.3235053
[12]	HUANG Z Q, ZHOU D H, SHEN Z W, et al. Directed graph-based topology derivation method for single-stage multiport inverters[J]. IEEE Transactions on Power Electronics, 2023, 38(11): 14614-14627. doi: 10.1109/TPEL.2023.3305988
[13]	CHEN Y, BAI J B, KANG Y. A nonisolated single-inductor multiport DC-DC topology deduction method based on reinforcement learning[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(6): 6572-6585. doi: 10.1109/JESTPE.2021.3128270
[14]	LI H, LI Y M, WANG W C, et al. Programmable topology deduction algorithm for S1D2C1L1 type DC-DC converters based on graph theory[C]//Proceedings of the 14th International FLINS Conference. Singapore: World Scientific, 2020.
[15]	李虹, 王文财, 李亚敏, 等. 基于图论的S¹D¹L²C¹型DC-DC变换器可编程拓扑搜索算法[J]. 中国电机工程学报, 2021, 41(16): 5670-5683. LI H, WANG W C, LI Y M, et al. Programmable topology searching algorithm for S¹D¹L²C¹ type DC-DC converters based on graph theory[J]. Proceedings of the CSEE, 2021, 41(16): 5670-5683(in Chinese).
[16]	CHEN G P, JIN Z F, LIU Y W, et al. Programmable topology derivation and analysis of integrated three-port DC-DC converters with reduced switches for low-cost applications[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 6649-6660.
[17]	MO L P, HUANG J M, CHEN G P, et al. Computer-aided systematic topology derivation of single-inductor multi-input multi-output converters from working principle[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2022, 69(6): 2637-2649. doi: 10.1109/TCSI.2022.3159718
[18]	ERICKSON R W, MAKSIMOVIĆ D. Fundamentals of power electronics[M]. Berlin: Springer, 2001.
[19]	张永, 李睿, 年福忠. 算法与数据结构[M]. 北京: 国防工业出版社, 2008. ZHANG Y, LI R, NIAN F Z. Algorithms and data structures[M]. Beijing: National Defense Industry Press, 2008(in Chinese).
[20]	XIE B Z, QI C, BEN H Q, et al. The applications of graph theory in electric network[C]//Proceedings of the International Conference on Sensing, Diagnostics, Prognostics, and Control. Piscataway: IEEE Press, 2019: 780-784.