Discrimination on isomorphism and equivalence of topologies of power electronics converters
-
摘要:
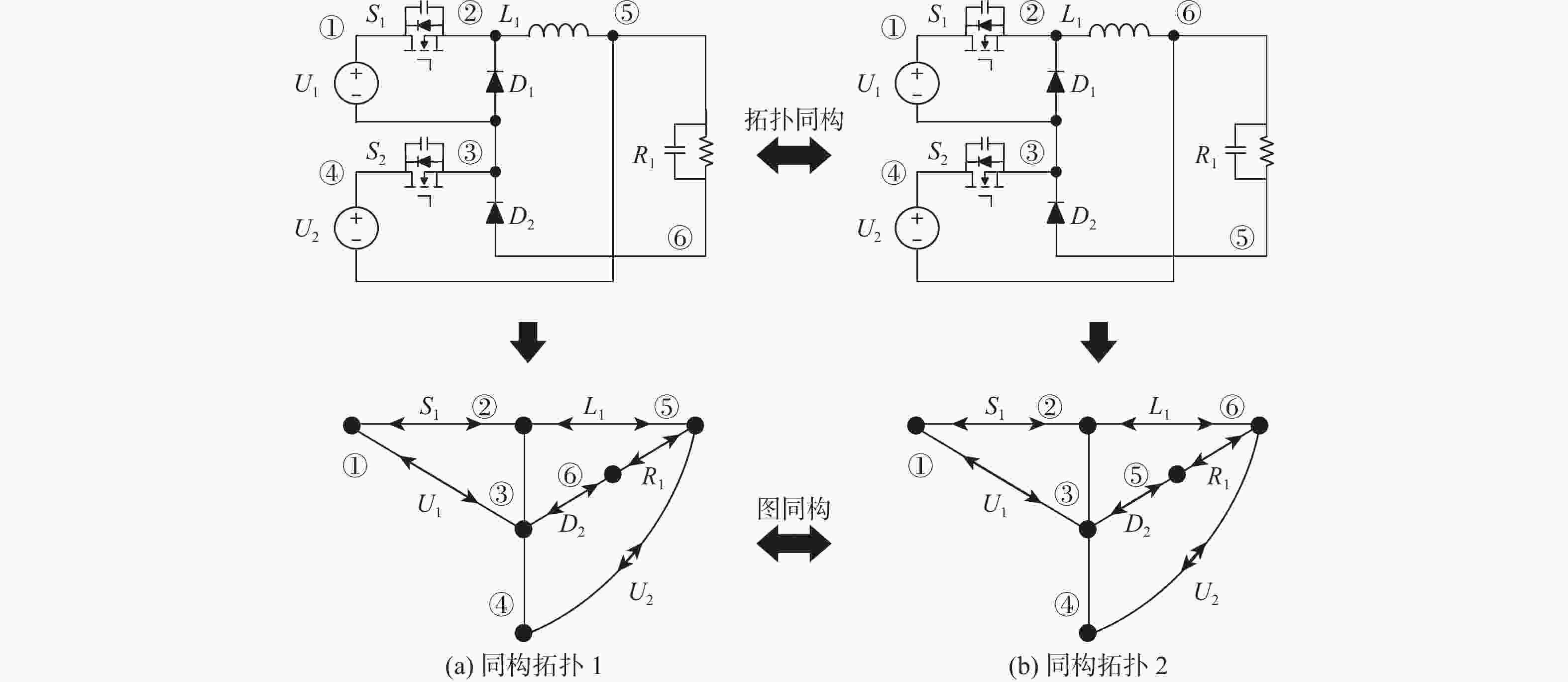
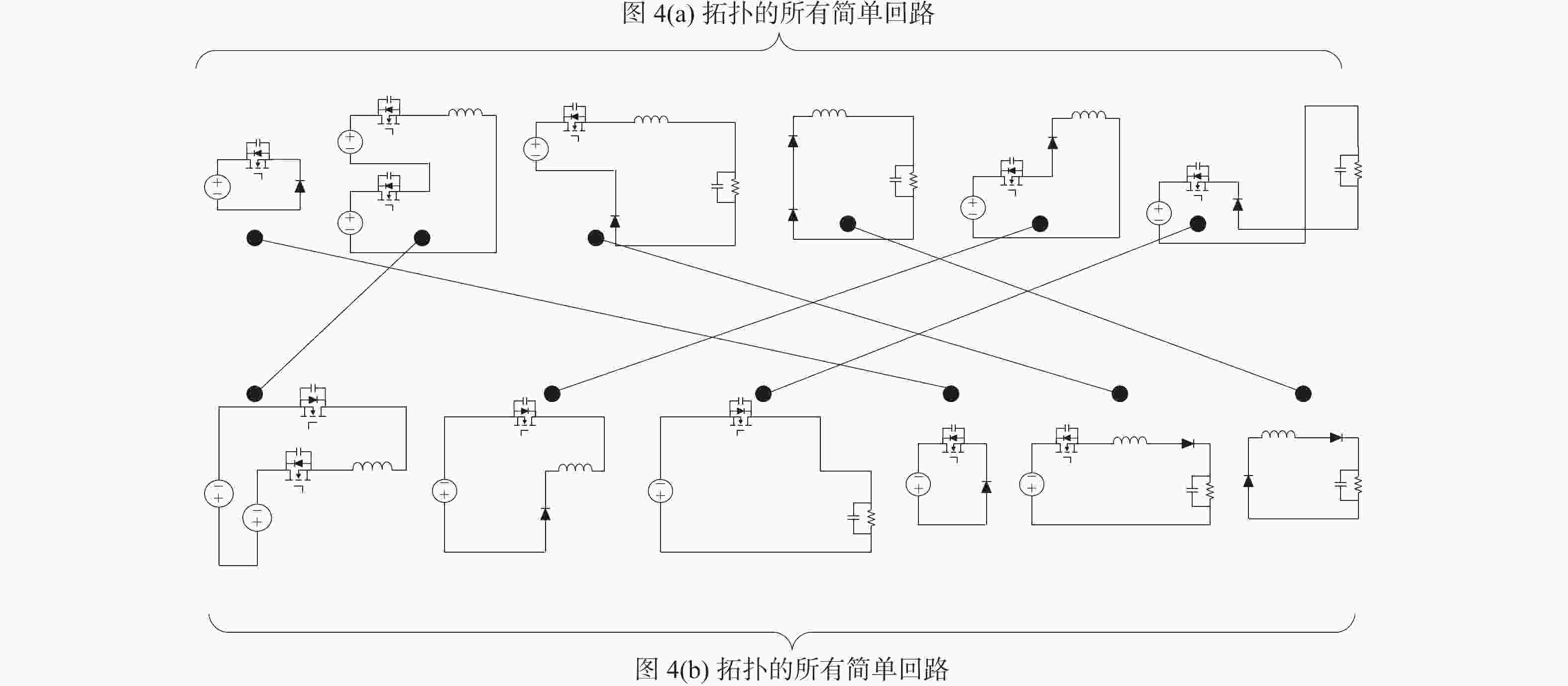
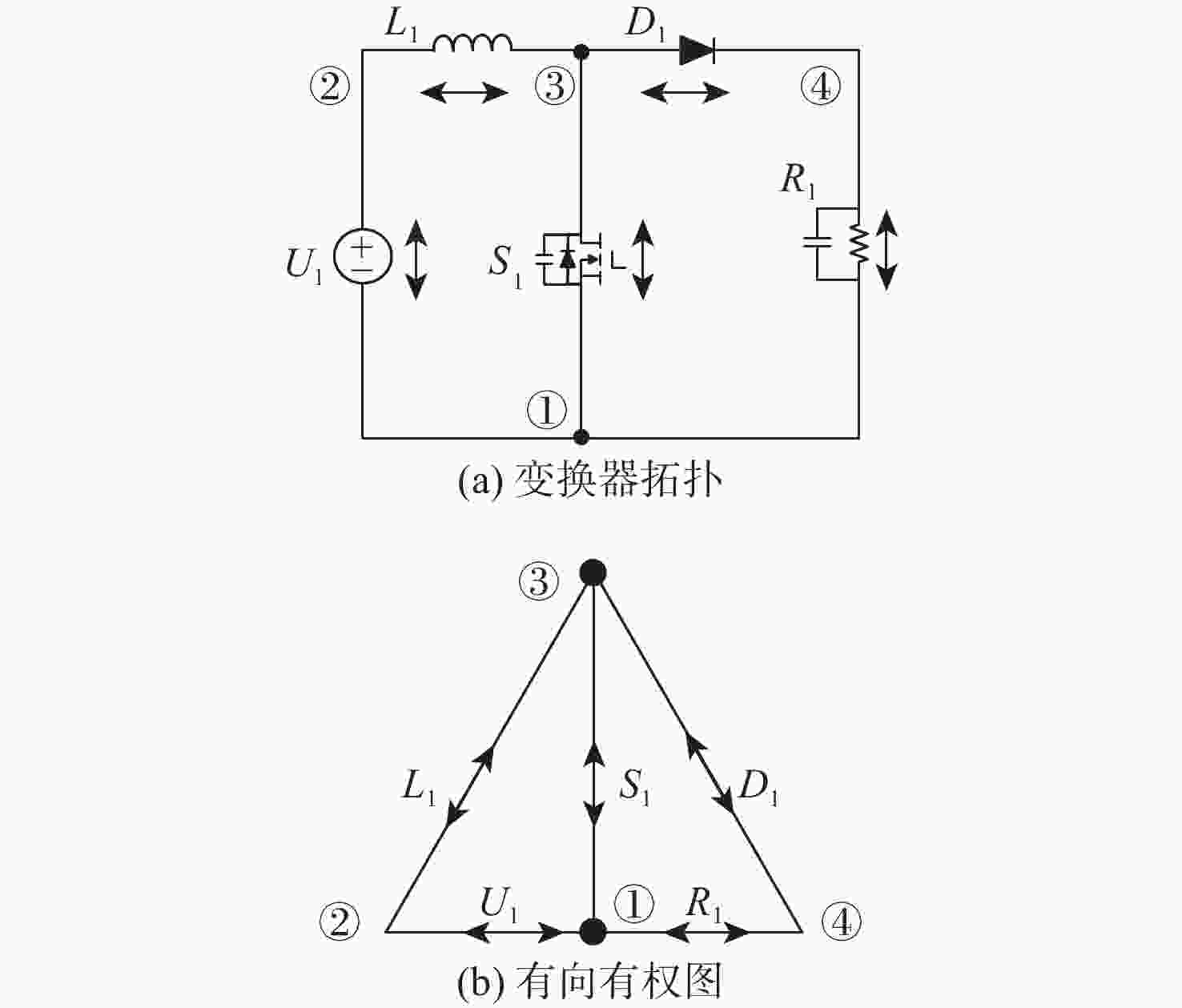
在电力电子变换器拓扑的推演过程中，通过拓扑等效或拓扑同构来识别结构不同但性能相同的拓扑，以避免重复研究，但拓扑等效与拓扑同构的内涵存在显著区别，容易导致混淆。为明确二者的区别与联系，提出准确识别性能相同拓扑的方法。推导出拓扑同构的必要条件为其邻接矩阵的行列式相等，并进一步推导出拓扑等效的充要条件为元件组成相同且简单回路一一对应；从拓扑子图的角度分析两者关系，发现拓扑同构是拓扑等效的充分非必要条件，而拓扑等效是性能相同拓扑的充要条件。基于此，建议实际应用中优先采用拓扑等效识别性能相同的拓扑。通过案例分析验证了理论的正确性和可行性。同时，提出了一种基于深度优先搜索算法实现等效拓扑自动判定的方法，为快速、准确识别性能相同的变换器拓扑提供了技术支持。
Abstract:In the process of deriving topologies for power electronic converters, researchers often use topology equivalence or topology isomorphism to identify topologies with different structures but identical performance, thereby avoiding redundant studies. However, the connotations of topology equivalence and topology isomorphism differ significantly, which can easily lead to confusion. To address this issue, this paper aims to clarify the distinctions and connections between the two concepts and propose a method for accurately identifying topologies with identical performance. First, it is deduced that a necessary condition for topology isomorphism is that their adjacency matrices have the same determinant. Furthermore, it is derived that the necessary and sufficient condition for topology equivalence is that the components are identical and the fundamental loops correspond one-to-one. Subsequently, an analysis from the perspective of topology subgraphs reveals that topology isomorphism is a sufficient but not necessary condition for topology equivalence, while topology equivalence is a necessary and sufficient condition for identical performance. Based on this, the paper recommends prioritizing topology equivalence over topology isomorphism in practical applications to identify topologies with identical performance. The theoretical results are validated through case studies demonstrating their correctness and feasibility. Additionally, this paper proposes a method based on the depth-first search algorithm to automatically determine equivalent topologies, enabling the rapid and accurate identification of converter topologies with identical performance.
-
图 3 2个同构的变换器拓扑及其对应的图
Figure 3. Two isomorphic converter topologies and their corresponding graphs
图 6 邻接矩阵行列式某项与简单回路的对应关系
Figure 6. Corresponding relationship between each item in determinant of adjacent matrix and simple loop
图 7 邻接矩阵行列式某项与2个不相连元件的对应关系
Figure 7. Corresponding relationship between each item in determinant of adjacent matrix and two disconnected components
图 8 用于案例分析的三端口变换器拓扑
Figure 8. Topologies of two three-port converter for case analysis
-
[1] ZHANG G D, LI Z, ZHANG B, et al. Power electronics converters: past, present and future[J]. Renewable and Sustainable Energy Reviews, 2018, 81: 2028-2044. doi: 10.1016/j.rser.2017.05.290 [2] ELSAYAD N, MORADISIZKOOHI H, MOHAMMED O A. A new hybrid structure of a bidirectional DC-DC converter with high conversion ratios for electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2020, 69(1): 194-206. doi: 10.1109/TVT.2019.2950282 [3] GNANASAMBANDAM K, RATHORE A K, EDPUGANTI A, et al. Current-fed multilevel converters: an overview of circuit topologies, modulation techniques, and applications[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3382-3401. doi: 10.1109/TPEL.2016.2585576 [4] 荣德生, 孙瑄瑨. 高增益耦合电感组合Buck-Boost-Zeta变换器.[J]. 中国电机工程学报, 2020, 40(14): 4590-4601.RONG D S, SUN X J. High gain coupled inductance combination Buck-Boost-Zeta converter[J]. Proceedings of the CSEE, 2020, 40(14): 4590-4601(in Chinese). [5] DE ANDRADE J M, SALVADOR M A, COELHO R F, et al. General method for synthesizing high gain step-up DC-DC converters based on differential connections[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 13239-13254. doi: 10.1109/TPEL.2020.2996501 [6] GANJAVI A, GHOREISHY H, AHMAD A A. A novel single-input dual-output three-level DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2018, 65(10): 8101-8111. doi: 10.1109/TIE.2018.2807384 [7] LI X L, DONG Z, TSE C K, et al. Single-inductor multi-input multi-output DC-DC converter with high flexibility and simple control[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 13104-13114. doi: 10.1109/TPEL.2020.2991353 [8] KUMAR G G, KRISHNA M V S, KUMARAVEL S, et al. Multi-stage DC-DC converter using active LC2D network with minimum component[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2021, 68(3): 943-947. [9] MO L P, CHEN G P, HUANG J M. From components to converters: a fundamental topology derivation method for single-inductor multi-input multi-output converters based on graph theory[C]//Proceedings of the IEEE International Conference on Power Electronics, Computer Applications. Piscataway: IEEE Press, 2021: 458-463. [10] CHEN Y, BAI J B, KANG Y. A nonisolated single-inductor multiport DC-DC topology deduction method based on reinforcement learning[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(6): 6572-6585. doi: 10.1109/JESTPE.2021.3128270 [11] LI H, LI Y, WANG W, et al. Programmable topology deduction algorithm for S1D2C1L1 type DC-DC converters based on graph theory[C]//Proceedings of the 14th International FLINS Conference. Singapore: World Scientific, 2020. [12] 李虹, 王文财, 李亚敏, 等. 基于图论的S1D1L2C1型DC-DC变换器可编程拓扑搜索算法[J]. 中国电机工程学报, 2021, 41(16): 5670-5683.LI H, WANG W C, LI Y M, et al. Programmable topology searching algorithm for S1D1L2C1 type DC-DC converters based on graph theory[J]. Proceedings of the CSEE, 2021, 41(16): 5670-5683(in Chinese). [13] CHEN G P, JIN Z F, LIU Y W, et al. Programmable topology derivation and analysis of integrated three-port DC-DC converters with reduced switches for low-cost applications[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 6649-6660. [14] MO L P, HUANG J M, CHEN G P, et al. Computer-aided systematic topology derivation of single-inductor multi-input multi-output converters from working principle[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2022, 69(6): 2637-2649. doi: 10.1109/TCSI.2022.3159718 [15] 石勇, 杨旭, 何群, 等. 同构混合开关拓扑的辨识[J]. 中国电机工程学报, 2003, 23(11): 116-121. doi: 10.3321/j.issn:0258-8013.2003.11.024SHI Y, YANG X, HE Q, et al. Identification of isomorphic hybrid switching topology[J]. Proceedings of the CSEE, 2003, 23(11): 116-121(in Chinese). doi: 10.3321/j.issn:0258-8013.2003.11.024 [16] SHANG H L, LI F, TANG X D, et al. A new algorithm for isomorphism determination of undirected graphs-circuit simulation method[J]. Circuits, Systems, and Signal Processing, 2011, 30(5): 1115-1130. doi: 10.1007/s00034-010-9248-7 [17] 商慧亮, 刘洋, 柳志栋, 等. 改进电路模拟法的应用: 同构混合开关拓扑辨识[J]. 应用科学学报, 2014, 32(2): 199-208.SHANG H L, LIU Y, LIU Z D, et al. Application of optimized circuit simulation: identification of isomorphic hybrid switching[J]. Journal of Applied Sciences, 2014, 32(2): 199-208(in Chinese). [18] GROHE M, SCHWEITZER P. The graph isomorphism problem[J]. Communications of the ACM, 2020, 63(11): 128-134. doi: 10.1145/3372123 [19] LI Y Z, KUPRAT J, LI Y W, et al. Graph-theory-based derivation, modeling, and control of power converter systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(6): 6557-6571. doi: 10.1109/JESTPE.2022.3143437 [20] MERKYS A, VAITKUS A, GRYBAUSKAS A, et al. Graph isomorphism-based algorithm for cross-checking chemical and crystallographic descriptions[J]. Journal of Cheminformatics, 2023, 15(1): 25. doi: 10.1186/s13321-023-00692-1 [21] CHEN G P, MO L P, LIU Y W, et al. Computer-aided identification of equivalent power electronics converters[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 9374-9378. doi: 10.1109/TPEL.2019.2909544 [22] 肖位枢. 图论及其算法[M]. 北京: 航空工业出版社, 1993.XIAO W S. Graph theory and its algorithm[M]. Beijing: Aviation Industry Press, 1993(in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 221
- HTML全文浏览量: 39
- PDF下载量: 22
- 被引次数: 0
