基于差分进化算法的SIMO Buck变换器最优动态响应搜索

李丹; 崔文峰; 陈桂鹏

doi:10.13700/j.bh.1001-5965.2023.0356

基于差分进化算法的SIMO Buck变换器最优动态响应搜索

doi: 10.13700/j.bh.1001-5965.2023.0356

李丹^{1, 2},
崔文峰³,
陈桂鹏^{1, 2, ,}

1.
厦门大学深圳研究院，深圳 518000
2.
厦门大学航空航天学院，厦门 361000
3.
浙江飞航智能科技有限公司，杭州 311100

基金项目:

广东省基础与应用基础研究基金(2022A1515011616)；国家自然科学基金(51907172)

详细信息

通讯作者:
E-mail：cgp2017@xmu.edu.cn

中图分类号: TM461
计量
- 文章访问数: 263
- HTML全文浏览量: 72
- PDF下载量: 15
- 被引次数: 0
出版历程
- 收稿日期: 2023-06-14
- 录用日期: 2023-09-27
- 网络出版日期: 2024-01-12
- 整期出版日期: 2025-05-31

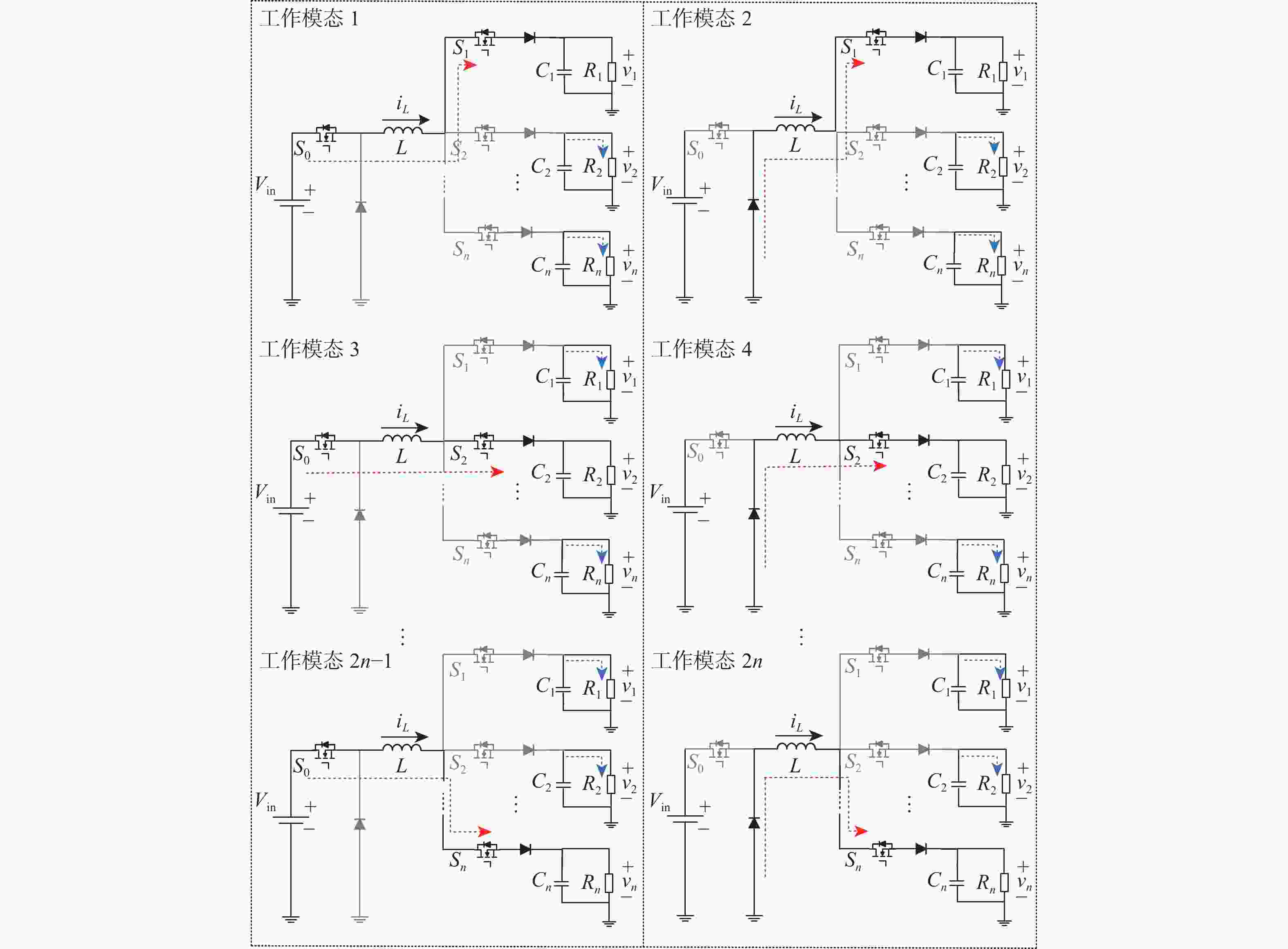
Optimal dynamic response exploration for SIMO Buck converter based on differential evolution algorithm

LI Dan^{1, 2},
CUI Wenfeng³,
CHEN Guipeng^{1, 2
, ,}

1.
Shenzhen Research Institute of Xiamen University，Shenzhen 518000，China
2.
School of Aerospace Engineering，Xiamen University，Xiamen 361000，China
3.
Zhejiang Feihang Intelligent Technology Co.，Ltd.，Hangzhou 311100，China

Funds:

Guangdong Basic and Applied Basic Research Foundation (2022A1515011616); National Natural Science Foundation of China (51907172)

More Information

Corresponding author: E-mail：cgp2017@xmu.edu.cn

摘要

摘要:
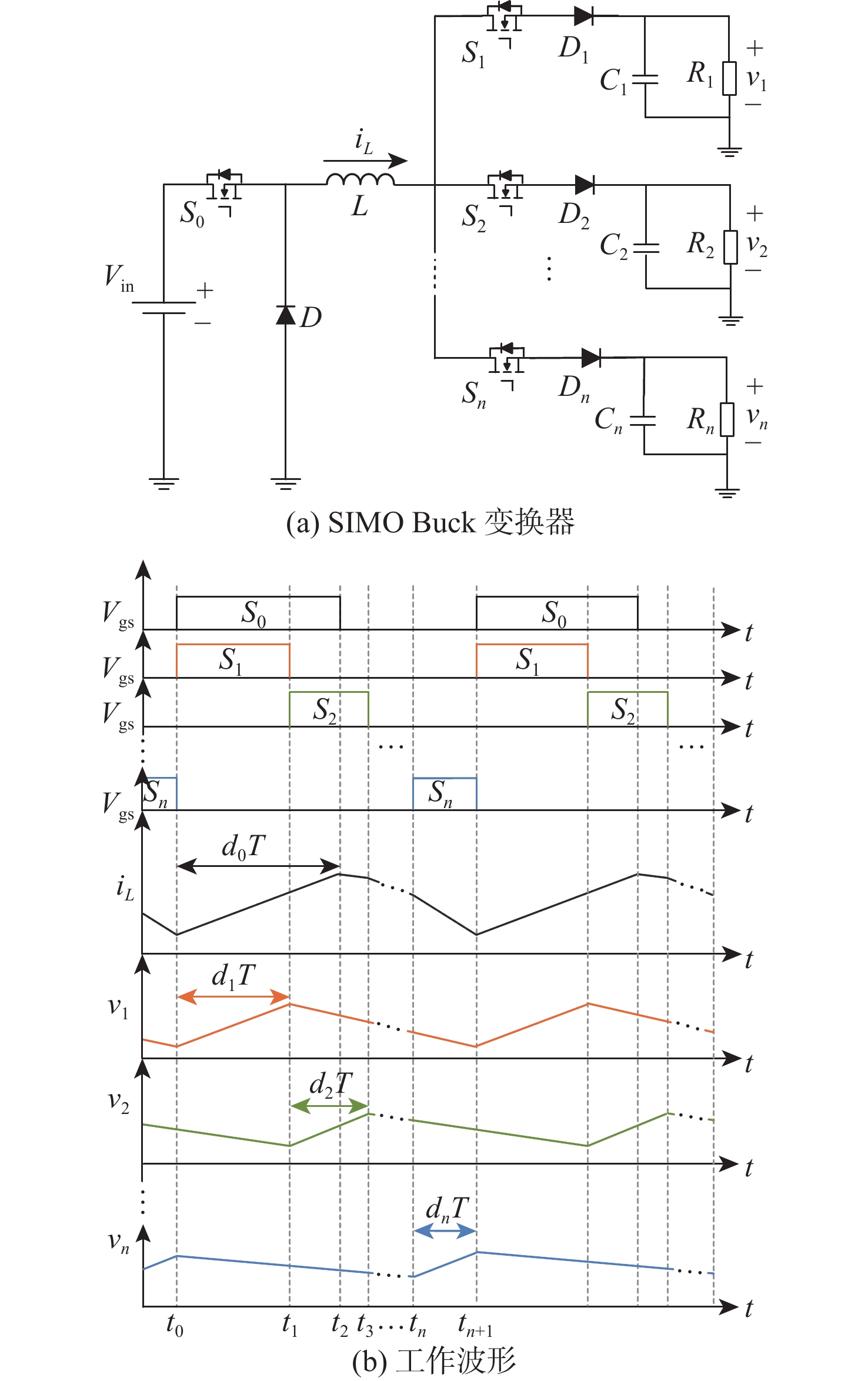
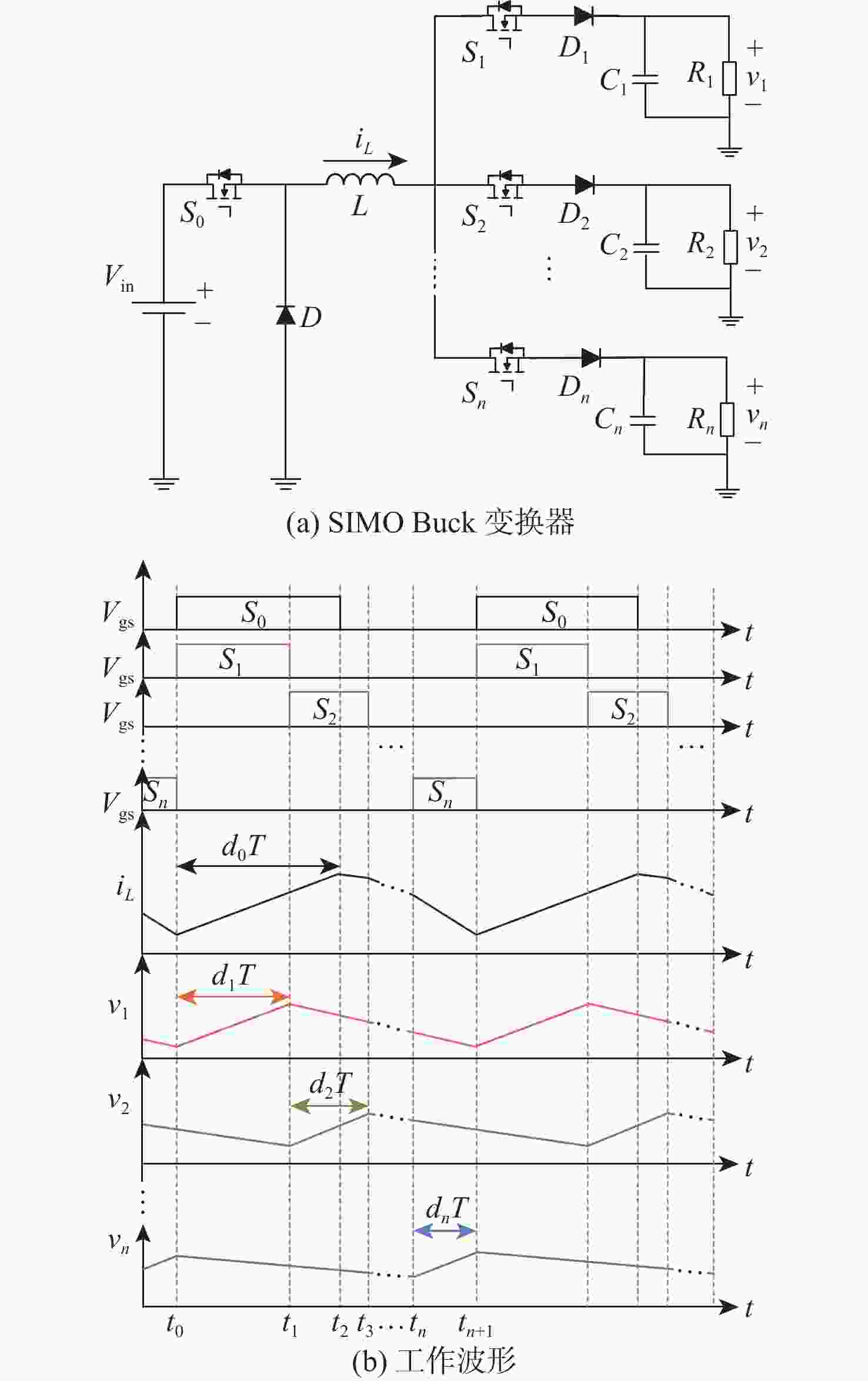
随着单电感多输出(SIMO)直流变换器的广泛应用，其动态响应问题备受关注。为探究SIMO Buck变换器最优动态响应的理论极限，根据变换器工作原理建立数学模型，利用改进的差分进化(DE)算法进行搜索求解。所提方法可以搜索求解出不同目标下的变换器最优动态响应要求，如最优的自调节或交叉调节，还可以获得不同约束下的最优动态响应，如不同的动态响应时间、峰值电感电流。基于启发式DE算法的最优动态响应理论极限搜索，有助于全面了解SIMO直流变换器的动态性能，并指导控制器设计以优化动态响应过程。
- 单电感多输出直流变换器 /
- 动态响应 /
- 差分进化算法 /
- 自调节 /
- 交叉调节
Abstract:
With the widespread application of single-inductor multiple-output (SIMO) DC-DC converters, their dynamic response has much concern for domestic and foreign researchers. To explore the theoretical limit of the optimal dynamic response for the SIMO Buck converter, this paper first establishes a corresponding mathematical model according to the working principle of the converter, and then an improved differential evolution (DE) algorithm is employed to search out the solution. In addition, the suggested approach can investigate the best dynamic response with various goals, including the best self-regulation or cross-regulation. It is also possible to know the optimal dynamic response with different constraints, such as different dynamic response times and peak inductor currents. In order to completely recognize the dynamic performance of SIMO DC-DC converters, the theoretical limit exploration of optimal dynamic response based on the heuristic DE intelligent algorithm is useful. Ideally, this will direct the controller design in order to obtain an optimized dynamic response.
- single-inductor multiple-output DC-DC converters /
- dynamic response /
- differential evolution algorithm /
- self-regulation /
- cross-regulation

HTML全文

图 1 SIMO Buck变换器和工作波形

Figure 1. SIMO Buck converter and operation waveform

下载: 全尺寸图片幻灯片

图 2 SIMO Buck变换器的工作模态

Figure 2. Operation mode of SIMO Buck converter

下载: 全尺寸图片幻灯片

图 3 负载R₁变化时使用PI控制和多变量控制的占空比d₁～d_n和输出电压v₁～v_n示意图

Figure 3. Duty cycles d₁～d_n and output voltages v₁～v_n using PI control and multivariable control when load R₁ varies

下载: 全尺寸图片幻灯片

图 4 改进DE算法进化流程

Figure 4. Evolution process of improved DE algorithm

下载: 全尺寸图片幻灯片

图 5 2种切载情况下，动态响应时间为7个周期的最优动态响应时电感电流和输出电压波形

Figure 5. Inductor current and output voltage when the optimal dynamic response is achieved with 7 periods under two load variations

下载: 全尺寸图片幻灯片

图 6 2种切载情况下，最优自调节时的电感电流和电压波形

Figure 6. Inductor current and output voltage when the optimal self-regulation is achieved under two load variations

下载: 全尺寸图片幻灯片

图 7 2种切载情况下，最优交叉调节时的电感电流和电压波形

Figure 7. Inductor current and output voltage when the optimal cross-regulation is achieved under two load variations

下载: 全尺寸图片幻灯片

图 8 2种切载情况下，动态响应时间为6个周期的最优动态响应时电感电流和输出电压波形

Figure 8. Inductor current and output voltage when the optimal dynamic response is achieved with 6 periods under two load variations

下载: 全尺寸图片幻灯片

图 9 2种切载情况下，不同动态响应时间的最优动态响应时电压波动变化曲线

Figure 9. Voltage fluctuation curves when the optimal dynamic response is achieved with different time under two load variations

下载: 全尺寸图片幻灯片

图 10 不同峰值电感电流约束的最优动态响应下电压波动变化曲线

Figure 10. Voltage fluctuation curves when the optimal dynamic response is achieved with different limited maximum inductor current

下载: 全尺寸图片幻灯片

图 11 峰值电感电流约束为11.3000 A和11.8000 A时最优动态响应的电感电流和电压波形

Figure 11. Inductor current and output voltage when the optimal dynamic response is achieved with maximum inductor current limited to 11.30000 A and 11.80000 A

下载: 全尺寸图片幻灯片

表 1 变换器电路参数

Table 1. Circuit parameters of converter

参数	数值
输入电压V_in/V	25
额定输出电压V_{1_ref}/V	5
额定输出电压V_{2_ref}/V	10
额定输出电压V_{3_ref}/V	15
电感L/μH	500
电容C₁，C₂，C₃/μF	1500
输出负载电阻R₁/Ω	1
输出负载电阻R₂，R₃/Ω	5

下载: 导出CSV

表 2 动态响应时间为7个周期时实现最优动态响应的占空比

Table 2. Duty cycles to achieve the optimal dynamic response when dynamic response time is 7 periods

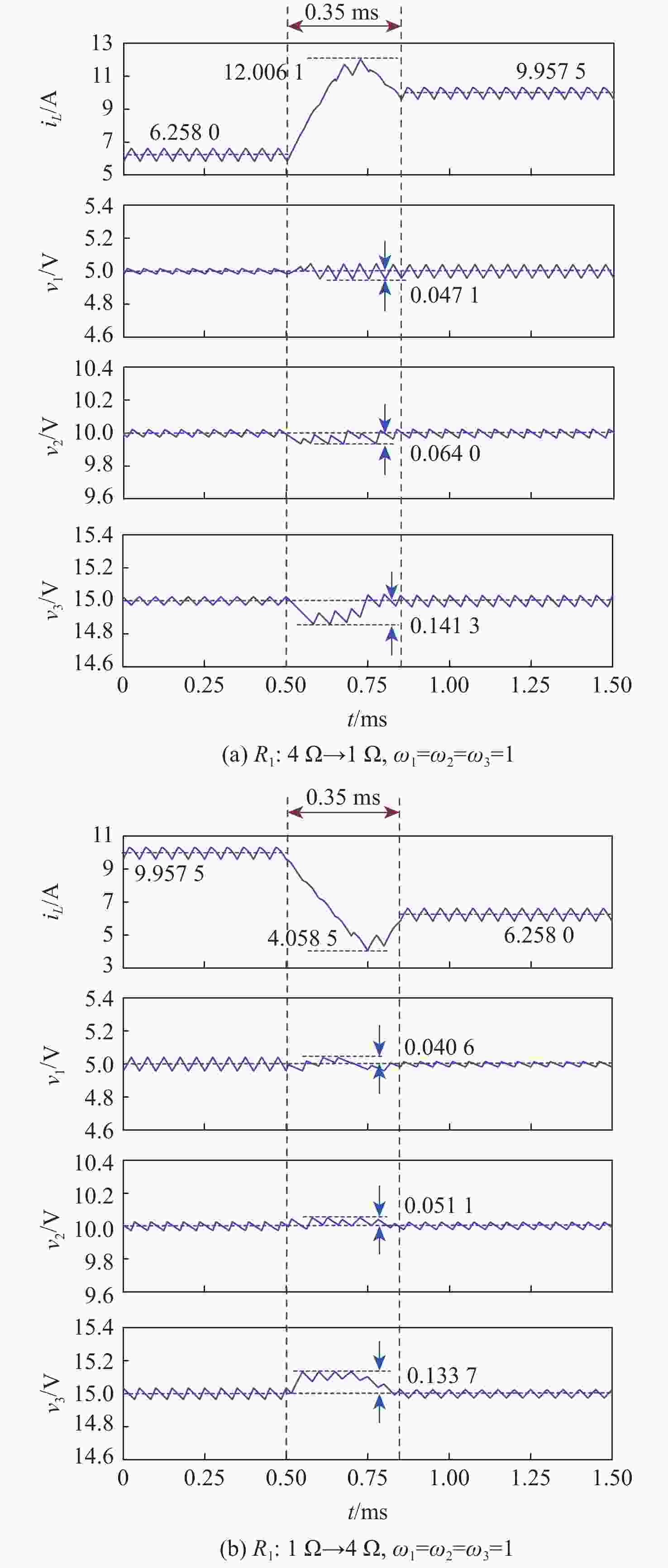
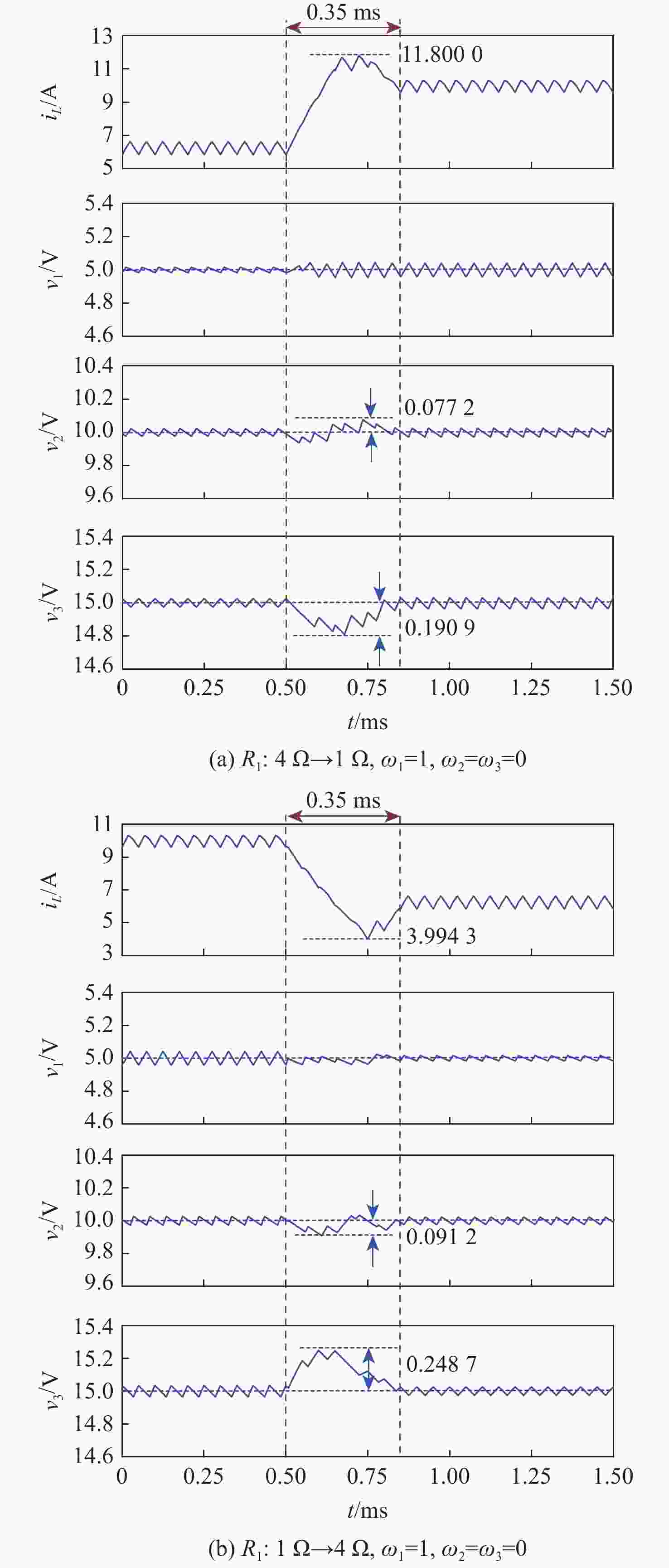
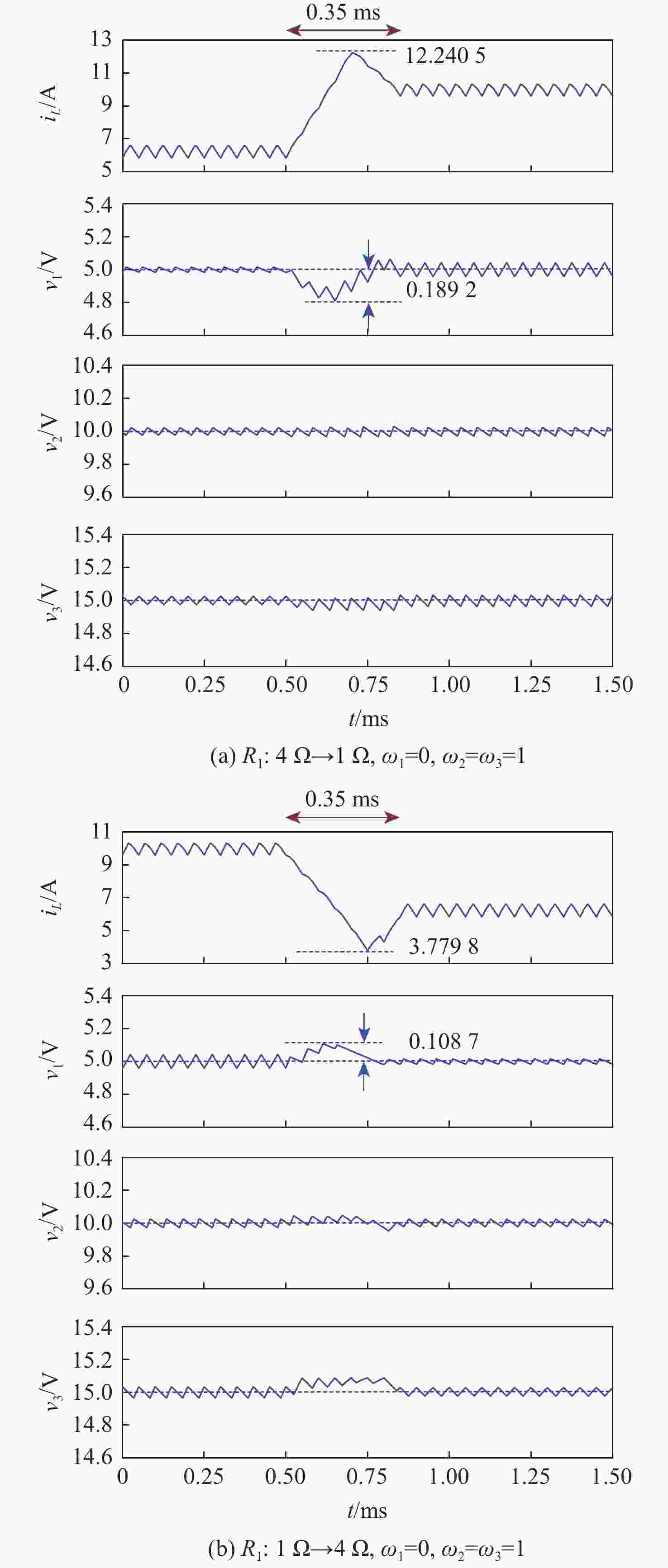
切载	开关管	占空比
切载	开关管	T	2T	3T	4T	5T	6T	7T
4 Ω → 1 Ω	S₀	1.000	0.997	0.924	0.505	0.490	0.060	0.001
	S₁	0.827	0.438	0.509	0.448	0.435	0.444	0.496
	S₂	0.173	0.231	0.179	0.254	0.091	0.264	0.218
1 Ω → 4 Ω	S₀	0.000	0.000	0.000	0.000	0.140	0.535	0.992
	S₁	0.135	0.251	0.265	0.191	0.020	0.237	0.406
	S₂	0.188	0.348	0.269	0.248	0.504	0.401	0.240

下载: 导出CSV

参考文献(25)

[1]	HUANG M H, CHEN K H. Single-inductor multi-output (SIMO) DC-DC converters with high light-load efficiency and minimized cross-regulation for portable devices[J]. IEEE Journal of Solid-State Circuits, 2009, 44(4): 1099-1111. doi: 10.1109/JSSC.2009.2014726
[2]	XU W W, LI Y, GONG X H, et al. A single-inductor dual-output switching converter with low ripples and improved cross regulation[C]//Proceedings of the IEEE Custom Integrated Circuits Conference. Piscataway: IEEE Press, 2009: 303-306.
[3]	JING X C, MOK P K T, LEE M C. A wide-load-range single-inductor-dual-output boost regulator with minimized cross-regulation by constant-charge-auto-hopping (CCAH) control[C]//Proceedings of the IEEE Custom Integrated Circuits Conference. Piscataway: IEEE Press, 2009: 299-302.
[4]	MA D S, KI W H, TSUI C Y, et al. Single-inductor multiple-output switching converters with time-multiplexing control in discontinuous conduction mode[J]. IEEE Journal of Solid-State Circuits, 2003, 38(1): 89-100. doi: 10.1109/JSSC.2002.806279
[5]	MA D S, KI W H, TSUI C Y. A pseudo-CCM/DCM SIMO switching converter with freewheel switching[J]. IEEE Journal of Solid-State Circuits, 2003, 38(6): 1007-1014. doi: 10.1109/JSSC.2003.811976
[6]	MA D S, KI W H. Fast-transient PCCM switching converter with freewheel switching control[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2007, 54(9): 825-829. doi: 10.1109/TCSII.2007.900903
[7]	TREVISAN D, MATTAVELLI P, TENTI P. Digital control of single-inductor multiple-output step-down DC-DC converters in CCM[J]. IEEE Transactions on Industrial Electronics, 2008, 55(9): 3476-3483. doi: 10.1109/TIE.2008.921234
[8]	WANG W, XU J P, WEI X J, et al. Peak inductor current and differential-mode voltage control of single-inductor dual-output buck converters in continuous conduction mode[C]//Proceedings of the IEEE 6th International Power Electronics and Motion Control Conference. Piscataway: IEEE Press, 2009: 495-499.
[9]	WANG Y, XU J P, YIN G. Cross-regulation suppression and stability analysis of capacitor current ripple controlled SIDO CCM Buck converter[J]. IEEE Transactions on Industrial Electronics, 2019, 66(3): 1770-1780. doi: 10.1109/TIE.2018.2838103
[10]	王瑶. 电容电流-电容电压纹波控制单电感双输出CCM Buck变换器[J]. 中国电机工程学报, 2020, 40(10): 3280-3288. WANG Y. Capacitor current and capacitor voltage ripple controlled single-inductor dual-output CCM Buck converter[J]. Proceedings of the CSEE, 2020, 40(10): 3280-3288(in Chinese).
[11]	WANG Y, XU J P, ZHOU G H. A cross regulation analysis for single-inductor dual-output CCM Buck converters[J]. Journal of Power Electronics, 2016, 16(5): 1802-1812. doi: 10.6113/JPE.2016.16.5.1802
[12]	PATRA P, GHOSH J, PATRA A. Control scheme for reduced cross-regulation in single-inductor multiple-output DC-DC converters[J]. IEEE Transactions on Industrial Electronics, 2013, 60(11): 5095-5104. doi: 10.1109/TIE.2012.2227895
[13]	DASIKA J D, BAHRANI B, SAEEDIFARD M, et al. Multivariable control of single-inductor dual-output Buck converters[J]. IEEE Transactions on Power Electronics, 2014, 29(4): 2061-2070. doi: 10.1109/TPEL.2013.2266616
[14]	LE H P, CHAE C S, LEE K C, et al. A single-inductor switching DC-DC converter with five outputs and ordered power-distributive control[J]. IEEE Journal of Solid-State Circuits, 2007, 42(12): 2706-2714. doi: 10.1109/JSSC.2007.908767
[15]	WOO Y J, LE H P, CHO G H, et al. Load-independent control of switching DC-DC converters with freewheeling current feedback[J]. IEEE Journal of Solid-State Circuits, 2008, 43(12): 2798-2808. doi: 10.1109/JSSC.2008.2005709
[16]	贺素霞, 张具琴. 基于模型预测控制单电感双输出Buck变换器的仿真分析[J]. 可再生能源, 2022, 40(4): 558-563. HE S X, ZHANG J Q. Simulation analysis of single inductor dual output Buck converter based on model predictive control[J]. Renewable Energy Resources, 2022, 40(4): 558-563(in Chinese).
[17]	WANG B F, TAN K T, SO P L. Low cross regulation SIMO DC/DC converter with model predictive voltage control[C]//Proceedings of the IEEE Power & Energy Society General Meeting. Piscataway: IEEE Press, 2013: 1-5.
[18]	WANG B F, KANAMARLAPUDI V R K, XIAN L, et al. Model predictive voltage control for single-inductor multiple-output DC-DC converter with reduced cross regulation[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4187-4197. doi: 10.1109/TIE.2016.2532846
[19]	ZHANG X N, WANG B F, TAN X J, et al. Deadbeat control for single-inductor multiple-output DC-DC converter with effectively reduced cross regulation[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(4): 3372-3381. doi: 10.1109/JESTPE.2019.2950247
[20]	TIAN M N, GAO X B, DAI C. Differential evolution with improved individual-based parameter setting and selection strategy[J]. Applied Soft Computing, 2017, 56: 286-297. doi: 10.1016/j.asoc.2017.03.010
[21]	WANG S H, LI Y Z, YANG H Y, et al. Self-adaptive differential evolution algorithm with improved mutation strategy[J]. Soft Computing, 2018, 22(10): 3433-3447. doi: 10.1007/s00500-017-2588-5
[22]	HOU Y, ZHAO L, LU H W. Fuzzy neural network optimization and network traffic forecasting based on improved differential evolution[J]. Future Generation Computer Systems, 2018, 81: 425-432. doi: 10.1016/j.future.2017.08.041
[23]	李笠, 李广鹏, 常亮, 等. 约束进化算法及其应用研究综述[J]. 计算机科学, 2021, 48(4): 1-13. LI L, LI G P, CHANG L, et al. Survey of constrained evolutionary algorithms and their applications[J]. Computer Science, 2021, 48(4): 1-13(in Chinese).
[24]	NOMAN N, IBA H. constrained differential evolution for economic dispatch with valve-point effect[J]. International Journal of Bio-Inspired Computation, 2011, 3(6): 346. doi: 10.1504/IJBIC.2011.043607
[25]	TAKAHAMA T, SAKAI S. Fast and stable constrained optimization by the ε constrained differential evolution[J]. Pacific Journal of Optimizatin, 2009, 5(2): 261-282.