Comprehensive evaluation of DC-DC converters based on analytic hierarchy process and entropy method
-
摘要:
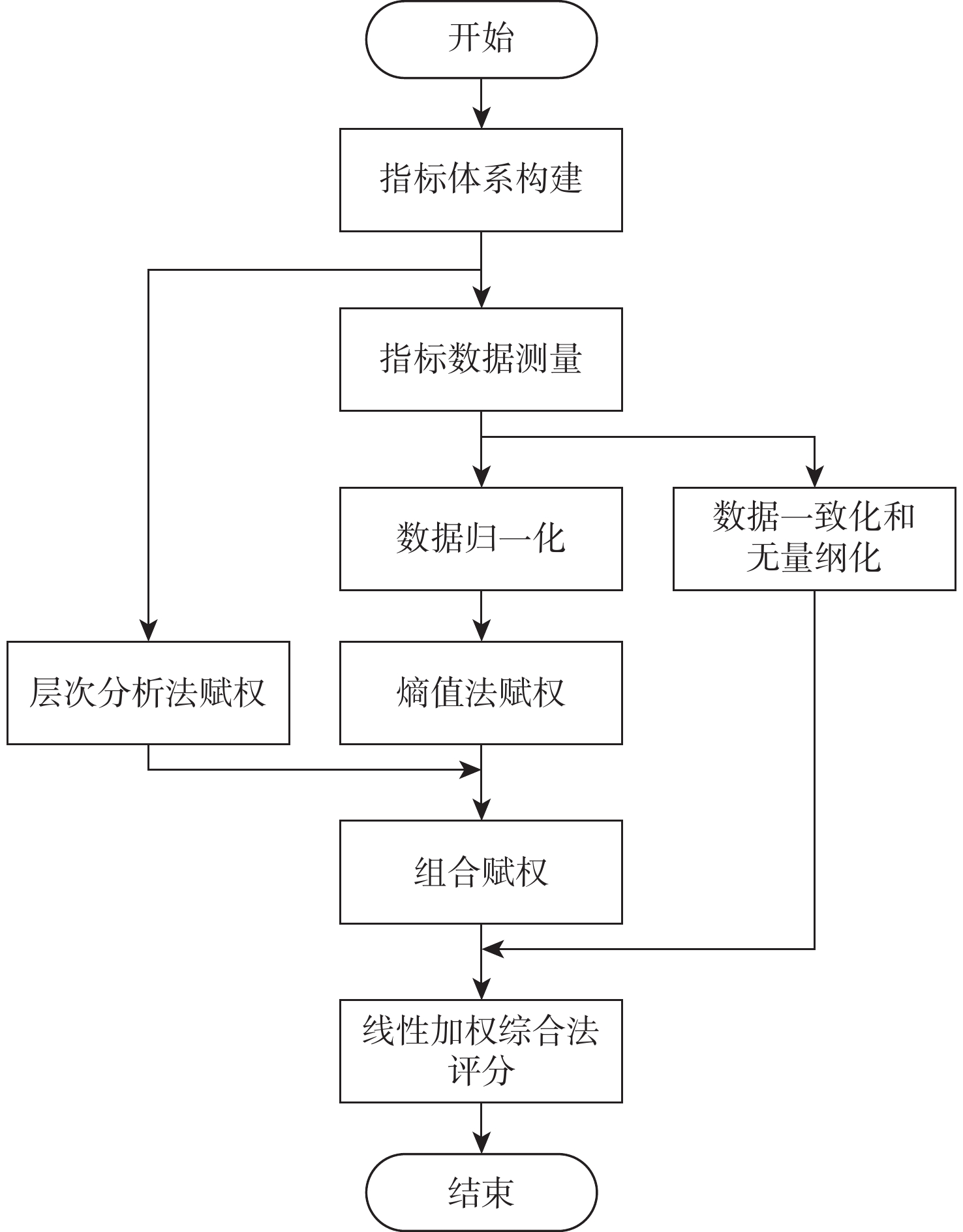
为了更全面地比较拓扑结构和功能相似的一系列DC-DC变换器并实现选优，提出了一种基于层次分析-熵值法的DC-DC变换器拓扑综合评价方法。通过总结DC-DC变换器的常用性能指标，构建分层次的评价指标体系；分别运用层次分析法和熵值法对指标体系中的指标赋权，并采用侧重于层次分析法的策略得到组合权重；进一步运用线性加权综合法得到各DC-DC变换器的评分。以11个电压增益均为
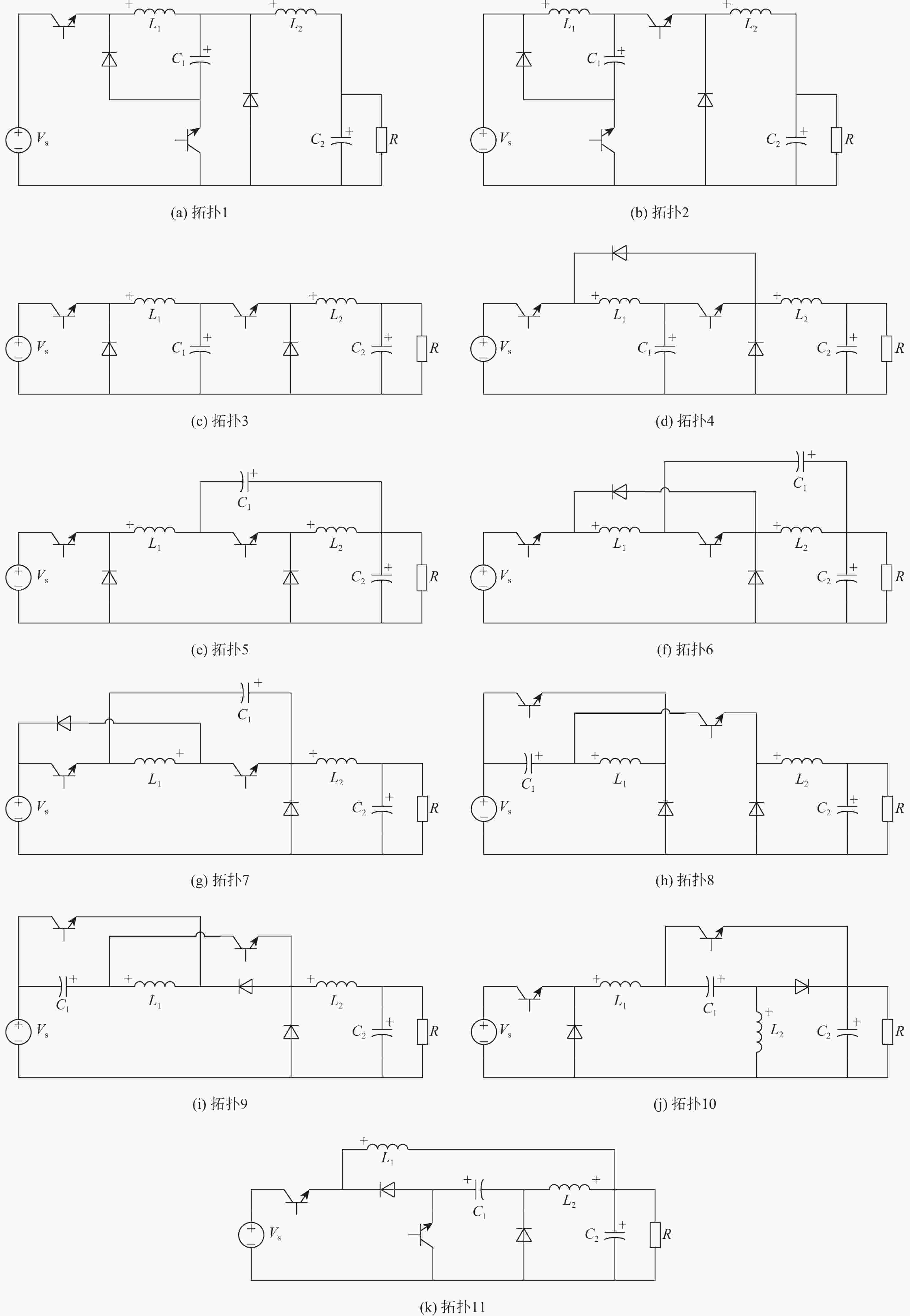
D 2的DC-DC变换器拓扑为例，运用所提方法进行综合评价，并对评价结果进行可行性分析，结果表明，所选出的拓扑具有良好性能。Abstract:In order to compare and optimize a series of DC-DC converters with similar topological structures and functions, a comprehensive topology evaluation method based on the analytic hierarchy process and entropy method is proposed. A hierarchical evaluation index system is created by compiling the common DC-DC converter performance indices. Analytic hierarchy process and entropy methods are used to assign weights to the indices in the index system, and the strategy focusing on analytic hierarchy process was adopted to get the combined weights. Additionally, each DC-DC converter’s evaluation value is obtained using the linear weighted average method. Finally, 11 DC-DC converters with a voltage gain of
D 2 are selected as the example to carry out a comprehensive evaluation using the proposed method, and a feasibility analysis of the evaluation result is given. The result indicates that the selected topologies have good performance.-
Key words:
- DC-DC converter /
- comprehensive evaluation /
- index system /
- analytic hierarchy process /
- entropy method
-
图 3 各拓扑评分值的雷达图
Figure 3. Radar chart of evaluation values of scores for each topologies
表 1 9级标度及其含义
Table 1. 9-level scale and its meaning
标度值 含义 1 Xi与Xj同等重要 3 Xi比Xj稍微重要 5 Xi比Xj明显重要 7 Xi比Xj强烈重要 9 Xi比Xj极端重要 2，4，6，8 重要性介于1，3，5，7，9之间 1～9的倒数 Xj比Xi重要，且cij=1/cji 
下载: 导出CSV
表 3 仿真参数
Table 3. Simulation parameters
参数 数值 输入电压/V 48 参考输出电压/V 12 占空比 0.5 开关管导通电阻/Ω 0.05 二极管导通压降/V 0.9 二极管导通电阻/Ω 0.01 负载电阻/Ω 3 开关频率/kHz 100
下载: 导出CSV
表 4 各二级指标判断矩阵的行平均值和指标权重
Table 4. Row averages of judgment matrix and weights of second level indices
行 行平均值 权重 A 2 0.3093 B 2 0.3093 C 1.2 0.1856 D 0.6333 0.0979 E 0.6333 0.0979
下载: 导出CSV
表 5 输出质量下各指标的行平均值和指标权重
Table 5. Row averages and weights of indices affiliated to “output quality”
行 行平均值 权重 A1 2.5 0.8 A2 0.625 0.2
下载: 导出CSV
表 6 层次分析法所得总权重
Table 6. Total weights obtained by AHP
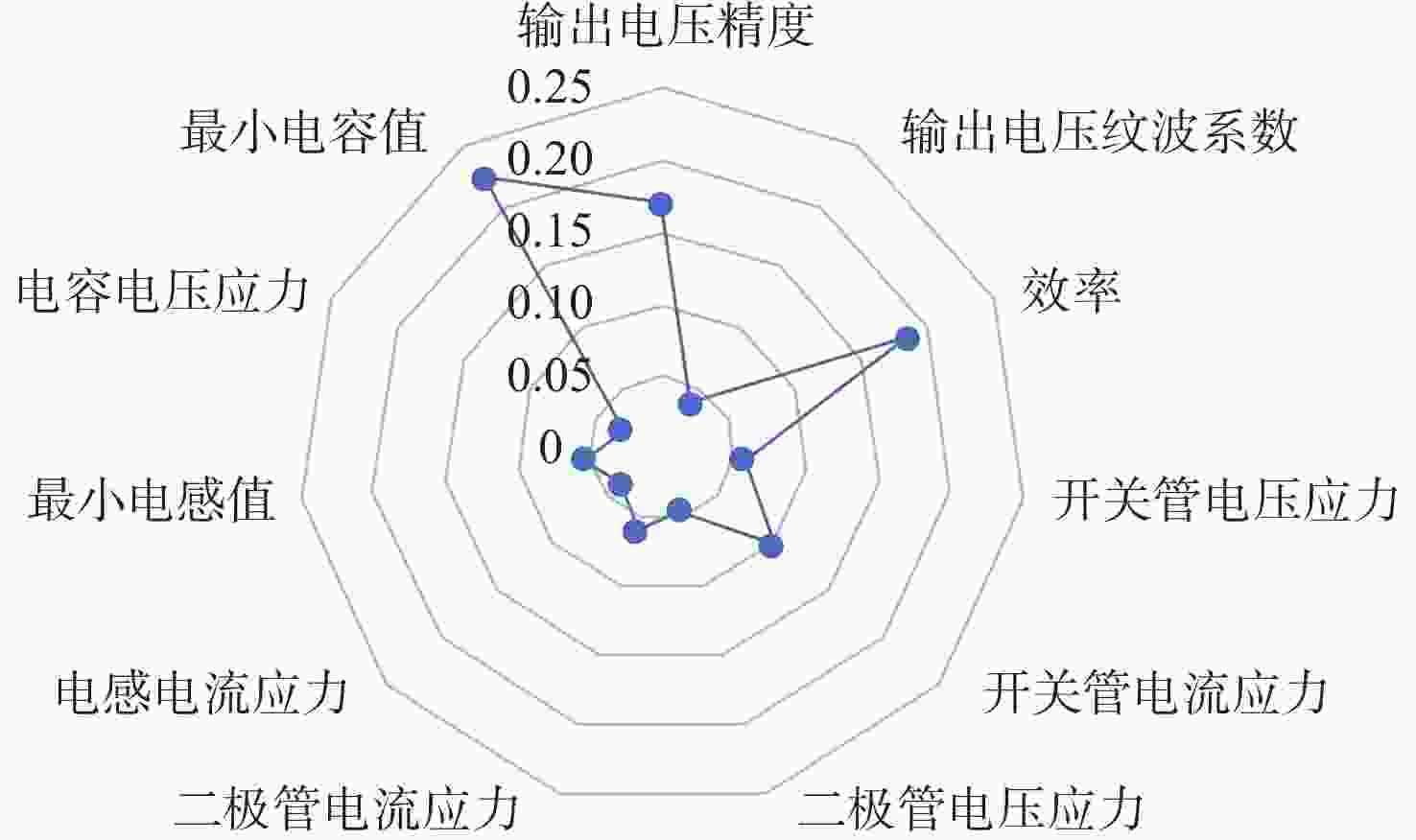
指标 权重 输出电压精度A1 0.2474 输出电压纹波系数A2 0.0619 效率B1 0.3093 开关管电压应力C1 0.0464 开关管电流应力C2 0.1392 二极管电压应力D1 0.0245 二极管电流应力D2 0.0735 电感电流应力E1 0.0326 最小电感值E2 0.0326 电容电压应力E3 0.0163 最小电容值E4 0.0163
下载: 导出CSV
A1 各拓扑的各项指标数值
A1. Index values of topologies
拓扑 输出电压
精度/%输出电压
纹波系数/%效率/% 开关管
电压应力/V开关管
电流应力/A二极管
电压应力/V二极管
电流应力/A电感电流
应力/A最小电
感值/μH电容电压
应力/V最小电
容值/μF1 6.193 0.987 91.002 49.04 2.265 35.79 3.345 3.386 101.200 17.483 28.370 2 6.454 1.001 90.523 61.21 3.365 35.76 3.34 3.378 101.200 17.470 28.370 3 6.627 0.987 90.395 36.725 3.405 35.685 3.335 3.372 101.200 17.432 28.370 4 8.773 1.001 90.000 36.98 3.3 24.095 4.36 3.288 104.392 17.067 28.355 5 6.688 1.006 90.322 36.725 3.405 35.685 3.335 3.369 101.200 11.802 80.266 6 8.667 0.999 90.065 36.99 3.3 24.095 4.365 3.292 104.392 11.571 80.208 7 8.185 0.958 89.377 37.01 3.3 24.105 4.37 3.290 104.392 18.066 26.908 8 5.621 0.949 89.432 36.775 3.42 35.735 3.345 3.385 101.200 17.961 27.633 9 8.170 1.045 90.180 37.01 3.335 24.105 4.405 3.326 104.392 18.069 26.908 10 5.924 0.984 91.146 36.76 3.43 35.72 3.355 2.259 161.921 17.509 28.370 11 6.170 0.988 91.026 49.04 2.265 35.79 3.345 2.254 161.921 17.483 28.370
下载: 导出CSV
A3 指标数值归一化
A3. Normalization of index values
拓扑 输出
电压精度输出电压
纹波系数效率 开关管
电压应力开关管
电流应力二极管
电压应力二极管
电流应力电感
电流应力最小
电感值电容
电压应力最小
电容值1 0.0799 0.0905 0.0916 0.1080 0.0651 0.1033 0.0818 0.0979 0.0811 0.0961 0.0688 2 0.0833 0.0918 0.0911 0.1347 0.0967 0.1032 0.0817 0.0976 0.0811 0.0960 0.0688 3 0.0855 0.0905 0.0910 0.0808 0.0979 0.1030 0.0815 0.0975 0.0811 0.0958 0.0688 4 0.1132 0.0918 0.0906 0.0814 0.0949 0.0695 0.1066 0.0950 0.0837 0.0938 0.0688 5 0.0863 0.0922 0.0909 0.0808 0.0979 0.1030 0.0815 0.0974 0.0811 0.0649 0.1948 6 0.1119 0.0916 0.0907 0.0814 0.0949 0.0695 0.1067 0.0952 0.0837 0.0636 0.1946 7 0.1057 0.0878 0.0900 0.0815 0.0949 0.0696 0.1068 0.0951 0.0837 0.0993 0.0653 8 0.0726 0.0870 0.0900 0.0810 0.0983 0.1031 0.0818 0.0978 0.0811 0.0987 0.0670 9 0.1055 0.0959 0.0908 0.0815 0.0959 0.0696 0.1077 0.0961 0.0837 0.0993 0.0653 10 0.0765 0.0902 0.0917 0.0809 0.0986 0.1031 0.0820 0.0653 0.1298 0.0962 0.0688 11 0.0796 0.0906 0.0916 0.1080 0.0651 0.1033 0.0818 0.0651 0.1298 0.0961 0.0688
下载: 导出CSV
表 7 指标的熵、偏差度和权重
Table 7. Entropy, deviations, and weights of indices
指标 熵 偏差度 权重 输出电压精度A1 0.9949 0.0051 0.0555 输出电压纹波系数A2 0.9999 0.0001 0.0013 效率B1 1 0 0.0001 开关管电压应力C1 0.9931 0.0069 0.0748 开关管电流应力C2 0.9959 0.0041 0.0445 二极管电压应力D1 0.9931 0.0069 0.0744 二极管电流应力D2 0.9964 0.0036 0.0395 电感电流应力E1 0.996 0.004 0.0439 最小电感值E2 0.9922 0.0078 0.0841 电容电压应力E3 0.9956 0.0044 0.0479 最小电容值E4 0.9508 0.0492 0.534
下载: 导出CSV
表 8 指标的组合权重
Table 8. Combined weights of indices
指标 权重 组合权重 层次分析法 熵值法 输出电压精度A1 0.2474 0.0555 0.1707 输出电压纹波系数A2 0.0619 0.0013 0.0376 效率B1 0.3093 0.0001 0.1856 开关管电压应力C1 0.0464 0.0748 0.0578 开关管电流应力C2 0.1392 0.0445 0.1013 二极管电压应力D1 0.0245 0.0744 0.0445 二极管电流应力D2 0.0735 0.0395 0.0599 电感电流应力E1 0.0326 0.0439 0.0372 最小电感值E2 0.0326 0.0841 0.0532 电容电压应力E3 0.0163 0.0479 0.0289 最小电容值E4 0.0163 0.534 0.2234
下载: 导出CSV
表 9 各拓扑的评分值
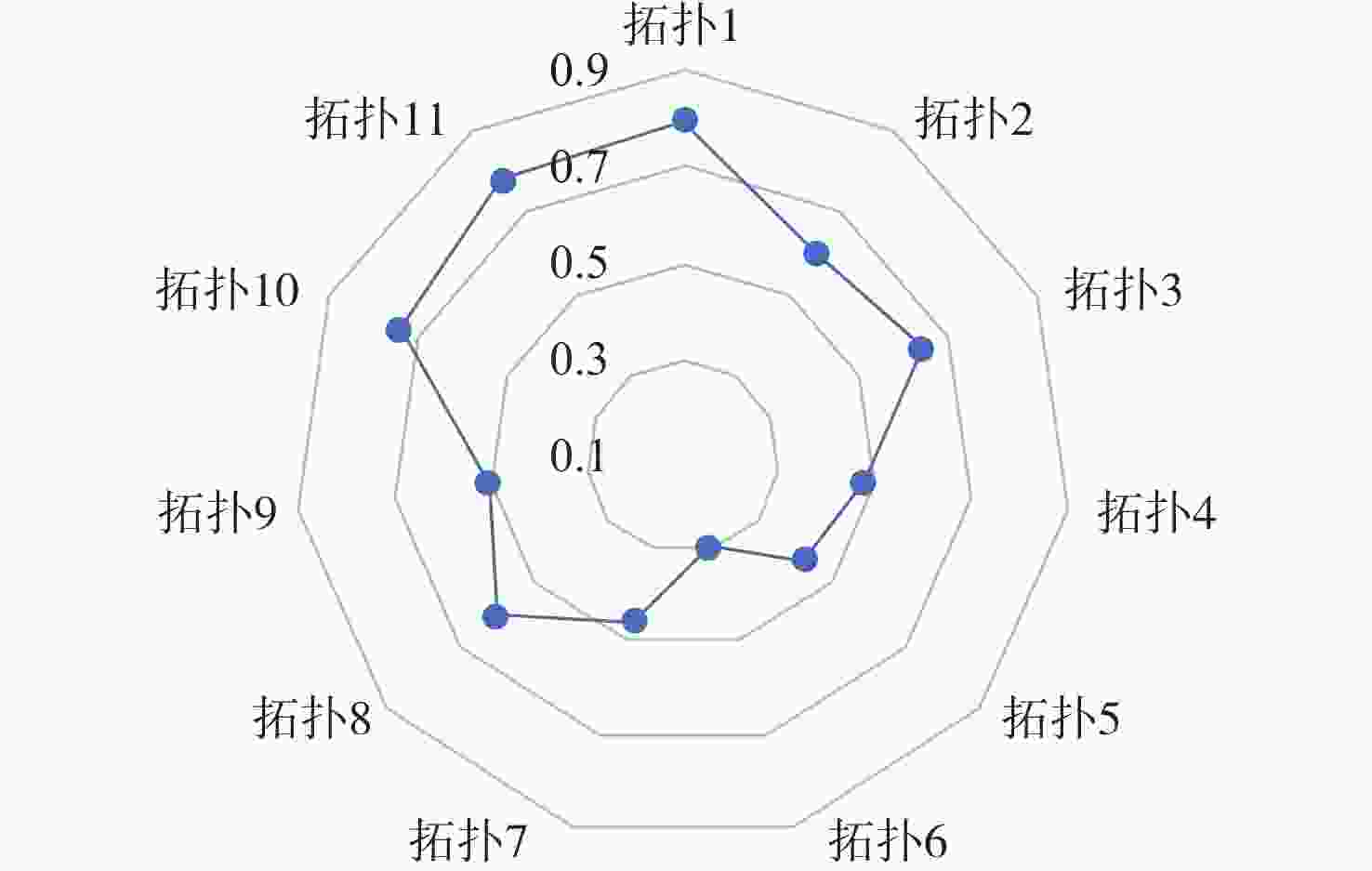
Table 9. Evaluation values of topologies
拓扑 评分值 1 0.7955 2 0.6018 3 0.6398 4 0.4736 5 0.4295 6 0.2939 7 0.4580 8 0.6062 9 0.5025 10 0.7372 11 0.7826
下载: 导出CSV
A2 指标数值一致化和无量纲化
A2. Harmonization and dimensionlessness of index values
拓扑 输出电
压精度输出电压
纹波系数效率 开关管
电压应力开关管
电流应力二极管
电压应力二极管
电流应力电感电
流应力最小
电感值电容
电压应力最小
电容值1 0.818662 0.607535 0.918425 0.497039 1 0 0.990654 0 1 0.090316 0.972584 2 0.73566 0.458493 0.647763 0 0.055794 0.002565 0.995327 0.006625 1 0.092243 0.972584 3 0.680941 0.606218 0.575519 1 0.021459 0.008978 1 0.012367 1 0.09816 0.972584 4 0 0.459766 0.352407 0.989585 0.111588 1 0.042056 0.086131 0.947438 0.154326 0.972875 5 0.66138 0.413818 0.534523 1 0.021459 0.008978 1 0.014576 1 0.964504 0 6 0.033836 0.481399 0.388856 0.989177 0.111588 1 0.037383 0.082597 0.947438 1 0.001078 7 0.186624 0.913162 0 0.988360 0.111588 0.999145 0.03271 0.084364 0.947438 0.000481 1 8 1 1 0.031351 0.997958 0.008584 0.004703 0.990654 0.000883 1 0.016646 0.986407 9 0.191383 0 0.454215 0.98836 0.081545 0.999145 0 0.052562 0.947438 0 1 10 0.90378 0.63679 1 0.998571 0 0.005985 0.981308 0.995141 0 0.086254 0.972584 11 0.8258 0.591535 0.93246 0.497039 1 0 0.990654 1 0 0.090201 0.972584
下载: 导出CSV
-
[1] 李虹, 王文财, 李亚敏, 等. 基于图论的S1D1L2C1型DC-DC变换器可编程拓扑搜索算法[J]. 中国电机工程学报, 2021, 41(16): 5670-5683.LI H, WANG W C, LI Y M, et al. Programmable topology searching algorithm for S1D1L2C1 type DC-DC converters based on graph theory[J]. Proceedings of the CSEE, 2021, 41(16): 5670-5683(in Chinese). [2] PANIGRAHI R, MISHRA S K, JOSHI A. Synthesis of an optimum converter topology for a specified voltage conversion ratio[J]. IEEE Transactions on Industry Applications, 2021, 57(4): 3923-3934. doi: 10.1109/TIA.2021.3081401 [3] CHEN Y, BAI J B, KANG Y. A nonisolated single-inductor multiport DC-DC topology deduction method based on reinforcement learning[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(6): 6572-6585. doi: 10.1109/JESTPE.2021.3128270 [4] MO L P, CHEN G P, HUANG J M, et al. Graph theory-based programmable topology derivation of multiport DC-DC converters with reduced switches[J]. IEEE Transactions on Industrial Electronics, 2022, 69(6): 5745-5755. doi: 10.1109/TIE.2021.3090711 [5] DONG M, LIANG R J, YANG J, et al. Topology derivation of multiport DC-DC converters based on reinforcement learning[J]. IEEE Transactions on Power Electronics, 2023, 38(4): 5055-5064. doi: 10.1109/TPEL.2023.3235053 [6] 何永秀, 刘敦楠, 罗涛, 等. 电力综合评价方法及应用[M]. 北京: 中国电力出版社, 2011: 13-194.HE Y X, LIU D N, LUO T, et al. Comprehensive evaluation method of electric power and its application[M]. Beijing: China Electric Power Press, 2011: 13-194(in Chinese). [7] 石宜金, 谭贵生, 赵波, 等. 基于模糊综合评估模型与信息融合的电力变压器状态评估方法[J]. 电力系统保护与控制, 2022, 50(21): 167-176.SHI Y J, TAN G S, ZHAO B, et al. Condition assessment method for power transformers based on fuzzy comprehensive evaluation and information fusion[J]. Power System Protection and Control, 2022, 50(21): 167-176(in Chinese). [8] 朱晓荣, 彭柏, 司羽, 等. 基于知识图谱的配电网综合评价[J]. 现代电力, 2022, 39(6): 677-684.ZHU X R, PENG B, SI Y, et al. Comprehensive evaluation of distribution network based on knowledge graph[J]. Modern Electric Power, 2022, 39(6): 677-684(in Chinese). [9] WANG J H, LIU S Q, WANG S X, et al. Multiple indicators-based health diagnostics and prognostics for energy storage technologies using fuzzy comprehensive evaluation and improved multivariate grey model[J]. IEEE Transactions on Power Electronics, 2021, 36(11): 12309-12320. doi: 10.1109/TPEL.2021.3075517 [10] 颜湘武, 赵帅帅, 董清, 等. 电动汽车充电机性能综合评估[J]. 电力系统保护与控制, 2020, 48(1): 164-171.YAN X W, ZHAO S S, DONG Q, et al. Comprehensive evaluation of electric vehicle charger performance[J]. Power System Protection and Control, 2020, 48(1): 164-171(in Chinese). [11] 王旭, 孟润泉, 韩肖清, 等. 基于改进AHP法-熵权法的交直流母线接口变换器综合性能评估[J]. 电网与清洁能源, 2021, 37(3): 8-16. doi: 10.3969/j.issn.1674-3814.2021.03.002WANG X, MENG R Q, HAN X Q, et al. Comprehensive performance evaluation of AC/DC bus interface converter based on improved AHP-entropy weight method[J]. Power System and Clean Energy, 2021, 37(3): 8-16(in Chinese). doi: 10.3969/j.issn.1674-3814.2021.03.002 [12] 曾晔, 加鹤萍, 杨菁, 等. 基于模糊层次分析法–熵权法–逼近理想解排序法的虚拟电厂综合贡献度评估方法[J]. 现代电力, 2024, 41(1): 144-151.ZENG Y, JIA H P, YANG J, et al. Comprehensive contribution degree evaluation method of virtual power plants based on FAHP-EWM-TOPSIS method[J]. Modern Electric Power, 2024, 41(1): 144-151(in Chinese). [13] 易平涛, 李伟伟, 郭亚军. 综合评价理论与方法[M]. 2版. 北京: 经济管理出版社, 2019: 12-83.YI P T, LI W W, GUO Y J. Comprehensive evaluation theory and methods[M]. 2nd ed. Beijing: Economy & Management Publishing House, 2019: 12-83(in Chinese). [14] 洪晟, 岳天羽, 李新建. 基于层次分析的信息物理网络多维攻击损毁评估[J]. 北京亚洲成人在线一二三四五六区学报, 2022, 48(9): 1827-1835.HONG S, YUE T Y, LI X J. Multidimensional attack damage assessment of cyber-physical systems based on hierarchical analysis[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(9): 1827-1835(in Chinese). [15] 付志扬, 王涛, 孔令号, 等. 基于AHP-TOPSIS算法的重要电力客户用电状态评估[J]. 电网技术, 2022, 46(10): 4095-4101.FU Z Y, WANG T, KONG L H, et al. Power consumption state evaluation of important power customers based on AHP-TOPSIS algorithm[J]. Power System Technology, 2022, 46(10): 4095-4101(in Chinese). [16] GE Q B, QIAO H Z, LI C X, et al. Real-time charging risk assessment for electric vehicles based on improved broad BP-AHP[J]. IEEE Transactions on Industrial Electronics, 2022, 69(9): 9472-9482. doi: 10.1109/TIE.2021.3111591 [17] 李敬强, 樊天辰, 周妍汝, 等. 基于云模型的民航监察员队伍能力综合评价[J]. 北京亚洲成人在线一二三四五六区学报, 2022, 48(12): 2425-2433.LI J Q, FAN T C, ZHOU Y R, et al. Comprehensive evaluation on capability of civil aviation supervisor team based on cloud model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(12): 2425-2433(in Chinese). [18] 黄伟, 杨子力, 柳思岐. 基于物元可拓模型的特色小镇能源系统综合评价[J]. 现代电力, 2020, 37(5): 448-457.HUANG W, YANG Z L, LIU S Q. Comprehensive energy system evaluation of new energy featured towns based on matter-element extension model[J]. Modern Electric Power, 2020, 37(5): 448-457(in Chinese). [19] 高书垚, 安泰, 宋剑. 基于熵权-正态云模型的智能电能表状态评估研究[J]. 电测与仪表, 2022, 59(1): 190-194.GAO S Y, AN T, SONG J. Status evaluation of smart meter based on entropy weight-normal cloud model[J]. Electrical Measurement & Instrumentation, 2022, 59(1): 190-194(in Chinese). [20] LIU Z Y, WANG Y S, CHENG Q X, et al. Analysis of the information entropy on traffic flows[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(10): 18012-18023. doi: 10.1109/TITS.2022.3155933 [21] 李智华, 张宇浩, 吴春华, 等. 基于动态指标的光伏组件健康程度诊断[J]. 电网技术, 2024, 48(2): 597-606.LI Z H, ZHANG Y H, WU C H, et al. Health diagnosis of photovoltaic modules based on dynamic health criteria[J]. Power System Technology, 2024, 48(2): 597-606(in Chinese). [22] 杜栋, 庞庆华, 吴炎. 现代综合评价方法与案例精选[M]. 3版. 北京: 清华大学出版社, 2015: 37-49.DU D, PANG Q H, WU Y. Modern comprehensive evaluation method and case selection[M]. 3rd ed. Beijing: Tsinghua University Press, 2015: 37-49(in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 500
- HTML全文浏览量: 143
- PDF下载量: 14
- 被引次数: 0
