非对称电网状态下MMC-HVDC改进滑模直接功率控制策略

关天一; 王怡博; 王睿; 赵海乔; 郑文婧; 孙秋野

doi:10.13700/j.bh.1001-5965.2023.0277

非对称电网状态下MMC-HVDC改进滑模直接功率控制策略

doi: 10.13700/j.bh.1001-5965.2023.0277

关天一^{1, 2},
王怡博¹,
王睿^1, ,,
赵海乔¹,
郑文婧³,
孙秋野¹

1.
东北大学信息科学与工程学院，沈阳 110819
2.
国网辽宁省电力有限公司沈阳供电公司，沈阳 110811
3.
国网辽宁省电力有限公司营销服务中心，沈阳 110168

基金项目:

国家自然科学基金(U20A20190,62073065)

详细信息

通讯作者:
E-mail：wangrui@ise.neu.edu.cn

中图分类号: TM46
计量
- 文章访问数: 451
- HTML全文浏览量: 64
- PDF下载量: 31
- 被引次数: 0
出版历程
- 收稿日期: 2023-05-25
- 录用日期: 2023-11-15
- 网络出版日期: 2023-12-06
- 整期出版日期: 2025-05-31

Improved sliding-mode direct power control strategy for MMC-HVDC under asymmetrical grid state

1.
College of Information Science and Engineering，Northeastern University，Shenyang 110819，China
2.
State Grid Liaoning Electric Power Co.，Ltd.，Shenyang Power Supply Company，Shenyang 110811，China
3.
State Grid Liaoning Electric Power Co.，Ltd.，Marketing Service Center，Shenyang 110168，China

Funds:

National Natural Science Foundation of China (U20A20190,62073065)

More Information

Corresponding author: E-mail：wangrui@ise.neu.edu.cn

摘要

摘要:
基于模块化多电平换流器的高压直流(MMC-HVDC) 输电系统是动态功率平衡系统，在非对称电网状态下，MMC的功率控制一般采用基于传统瞬时功率模型的双闭环矢量控制策略，存在控制结构复杂、控制精度低等问题。为此，引入柔性瞬时功率模型，以有功功率和柔性无功功率为控制对象建立通用功率方程，提出一种基于柔性瞬时功率模型的MMC-HVDC改进滑模直接功率控制策略。该策略结合柔性瞬时功率模型和改进滑模控制方法，消除非对称电网状态下MMC输出功率的波动分量，省略了电流内环与功率补偿项，优化了控制结构。仿真和实验结果表明：所提控制策略在非对称电网、参数摄动等运行工况下的动态响应能力、控制精度和鲁棒性更强，更能发挥出柔性瞬时功率模型的优势。
- 基于模块化多电平换流器的高压直流 /
- 非对称电网 /
- 滑模控制 /
- 柔性瞬时功率模型 /
- 鲁棒控制
Abstract:
The modular multilevel converter based high voltage direct current (MMC-HVDC) is a dynamic power balancing system. The control system of MMC generally adopts a dual closed-loop vector control strategy based on the traditional instantaneous power model under an asymmetric grid state, which has a complex control structure and low control accuracy. This paper introduces a flexible instantaneous power model and establishes a general power equation with active power and new reactive power as control objects. In order to eliminate the twice grid-frequency ripples in both active and reactive power under asymmetric grid states, an enhanced sliding-mode MMC-HVDC direct power control strategy based on the new instantaneous power model is proposed. This approach combines the improved sliding-mode control method with the flexible instantaneous power model. Furthermore, it omits the inner-loop controller and power compensation terms while optimizing the control structure. According to simulation results, the suggested approach can more effectively take advantage of the benefits of the flexible instantaneous power model because it has superior dynamic responsiveness, control precision, and robustness under operating conditions including asymmetric grid state and parameter perturbation.
- modular multilevel converter based high voltage direct current /
- asymmetrical grid /
- sliding mode control /
- flexible instantaneous power model /
- robust control

HTML全文

图 1 MMC等效电路

Figure 1. MMC equivalent circuit

下载: 全尺寸图片幻灯片

图 2 SMC的响应过程

Figure 2. Response process of SMC

下载: 全尺寸图片幻灯片

图 3 本文控制系统结构框图

Figure 3. Block diagram of the proposed control strategy

下载: 全尺寸图片幻灯片

图 4 四端MMC-HVDC系统

Figure 4. Four-terminal MMC-HVDC system

下载: 全尺寸图片幻灯片

图 5 对称电网条件下MMC2的稳态仿真情况

Figure 5. Steady-state simulation results of MMC2 under balanced grid condition

下载: 全尺寸图片幻灯片

图 6 非对称电网条件下MMC2的暂态运行情况

Figure 6. Transient operation results of MMC2 under asymmetric grid condition

下载: 全尺寸图片幻灯片

图 7 PI控制器、传统滑模控制器与改进滑模控制器的动态和鲁棒性控制效果对比

Figure 7. Comparison of control results of dynamic power responses and robustness using PI controller, conventional SMC and improved SMC

下载: 全尺寸图片幻灯片

图 8 MMC硬件在环实验平台

Figure 8. Hardware-in-the-loop experiment topology of MMC

下载: 全尺寸图片幻灯片

图 9 对称电网条件下MMC2的稳态实验结果

Figure 9. Steady-state experimental results of MMC2 under balanced grid condition

下载: 全尺寸图片幻灯片

图 10 非对称电网条件下MMC2的暂态实验结果

Figure 10. Transient operation experimental results of MMC2 under asymmetric grid condition

下载: 全尺寸图片幻灯片

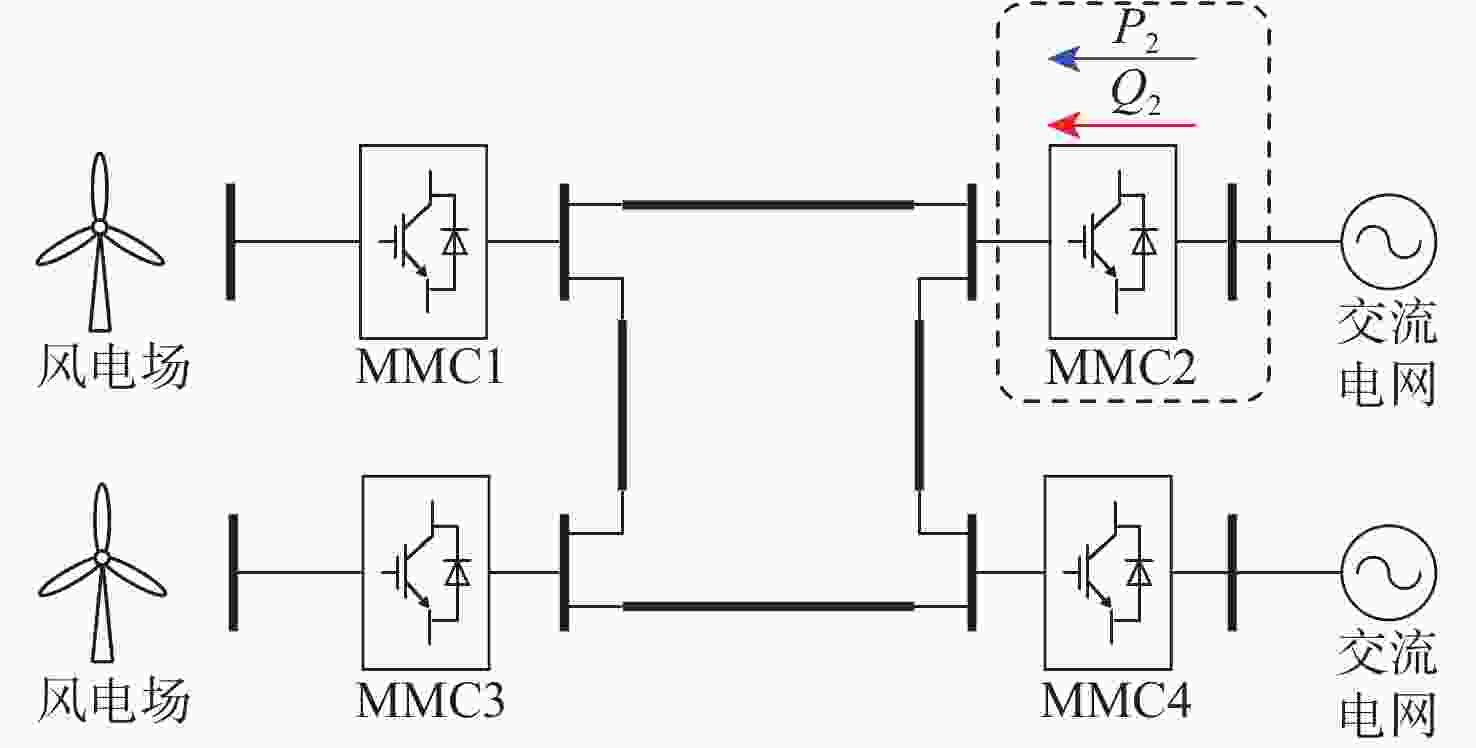
表 1 MMC2换流站参数

Table 1. Parameters of MMC2 converter station

参数数值

系统直流电压/kV ±200

交流线电压/kV 220

子模块电容/μF 8950

桥臂电感/mH 41.5

子模块数量/个 120

下载: 导出CSV

参考文献(30)

[1]	MUTHAVARAPU A K, BISWAS J, BARAI M. An efficient sorting algorithm for capacitor voltage balance of modular multilevel converter with space vector pulsewidth modulation[J]. IEEE Transactions on Power Electronics, 2022, 37(8): 9254-9265. doi: 10.1109/TPEL.2022.3160665
[2]	RAJU M N, SREEDEVI J, MANDI R P, et al. Modular multilevel converters technology: a comprehensive study on its topologies, modelling, control and applications[J]. IET Power Electronics, 2019, 12(2): 149-169. doi: 10.1049/iet-pel.2018.5734
[3]	MA K, HE B, XIN X K, et al. Capacitor voltage control for mission profile emulator of submodule in modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2021, 36(11): 12355-12364. doi: 10.1109/TPEL.2021.3082156
[4]	NAMI A, LIANG J Q, DIJKHUIZEN F, et al. Modular multilevel converters for HVDC applications: review on converter cells and functionalities[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 18-36. doi: 10.1109/TPEL.2014.2327641
[5]	管敏渊, 徐政. 模块化多电平换流器型直流输电的建模与控制[J]. 电力系统自动化, 2010, 34(19): 64-68. GUAN M Y, XU Z. Modeling and control of modular multilevel converter in HVDC transmission[J]. Automation of Electric Power Systems, 2010, 34(19): 64-68(in Chinese).
[6]	VASILADIOTIS M, CHERIX N, RUFER A. Accurate capacitor voltage ripple estimation and current control considerations for grid-connected modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2014, 29(9): 4568-4579. doi: 10.1109/TPEL.2013.2286293
[7]	李仪, 郭宏, 蔚永强. 永磁同步电动机大惯量负载的滑模变结构控制[J]. 北京亚洲成人在线一二三四五六区学报, 2007, 33(10): 1208-1211. doi: 10.3969/j.issn.1001-5965.2007.10.019 LI Y, GUO H, YU Y Q. Sliding mode control of permanent magnet synchronous motor with great inertia load[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(10): 1208-1211(in Chinese). doi: 10.3969/j.issn.1001-5965.2007.10.019
[8]	LI B, XIE Y Z, WEN W J, et al. Improved sliding-mode control for MMC in DC power system[J]. IET Renewable Power Generation, 2020, 14(15): 3035-3042. doi: 10.1049/iet-rpg.2020.0493
[9]	WANG S D, DRAGICEVIC T, GAO Y, et al. Machine learning based operating region extension of modular multilevel converters under unbalanced grid faults[J]. IEEE Transactions on Industrial Electronics, 2021, 68(5): 4554-4560. doi: 10.1109/TIE.2020.2982109
[10]	FREYTES J, LI J Q, DE PRÉVILLE G, et al. Grid-forming control with current limitation for MMC under unbalanced fault ride-through[J]. IEEE Transactions on Power Delivery, 2021, 36(3): 1914-1916. doi: 10.1109/TPWRD.2021.3053148
[11]	孔明, 汤广福, 贺之渊, 等. 不对称交流电网下MMC-HVDC输电系统的控制策略[J]. 中国电机工程学报, 2013, 33(28): 41-49. KONG M, TANG G F, HE Z Y, et al. A control strategy for modular multilevel converter based HVDC of unbalanced AC systems[J]. Proceedings of the CSEE, 2013, 33(28): 41-49(in Chinese).
[12]	陈海荣, 徐政. 基于同步坐标变换的VSC-HVDC暂态模型及其控制器[J]. 电工技术学报, 2007, 22(2): 121-126. doi: 10.3321/j.issn:1000-6753.2007.02.021 CHEN H R, XU Z. Transient model and controller design for VSC-HVDC based on synchronous reference frame[J]. Transactions of China Electrotechnical Society, 2007, 22(2): 121-126(in Chinese). doi: 10.3321/j.issn:1000-6753.2007.02.021
[13]	张建坡, 赵成勇, 敬华兵. 比例谐振控制器在MMC-HVDC控制中的仿真研究[J]. 中国电机工程学报, 2013, 33(21): 53-62. ZHANG J P, ZHAO C Y, JING H B. Simulating research of proportional resonant controllers in MMC-HVDC[J]. Proceedings of the CSEE, 2013, 33(21): 53-62(in Chinese).
[14]	SHANG L, SUN D, HU J. Sliding-mode-based direct power control of grid-connected voltage-sourced inverters under unbalanced network conditions[J]. IET Power Electronics, 2011, 4(5): 570-579. doi: 10.1049/iet-pel.2010.0160
[15]	年珩, 程鹏. 电网电压不平衡时PWM整流器的谐振直接功率控制策略[J]. 电工技术学报, 2013, 28(11): 86-94. doi: 10.3969/j.issn.1000-6753.2013.11.012 NIAN H, CHENG P. Resonant based direct power control strategy for PWM rectifier under unbalanced grid voltage condition[J]. Transactions of China Electrotechnical Society, 2013, 28(11): 86-94(in Chinese). doi: 10.3969/j.issn.1000-6753.2013.11.012
[16]	张迪, 魏艳君, 马利轩, 等. 不平衡电网电压下基于滑模变结构控制的双馈风电系统网侧变流器控制策略[J]. 电工技术学报, 2015, 30(10): 266-275. doi: 10.3969/j.issn.1000-6753.2015.10.036 ZHANG D, WEI Y J, MA L X, et al. Sliding-mode control for grid-side converters of DFIG-based wind-power generation system under unbalanced grid voltage conditions[J]. Transactions of China Electrotechnical Society, 2015, 30(10): 266-275(in Chinese). doi: 10.3969/j.issn.1000-6753.2015.10.036
[17]	梁营玉, 杨奇逊, 刘建政, 等. 电网电压不平衡时MMC-HVDC的无差拍直接功率控制[J]. 电工技术学报, 2015, 30(15): 15-25. doi: 10.3969/j.issn.1000-6753.2015.15.002 LIANG Y Y, YANG Q X, LIU J Z, et al. Deadbeat direct power control for MMC-HVDC under unbalanced grid voltages[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 15-25(in Chinese). doi: 10.3969/j.issn.1000-6753.2015.15.002
[18]	刘子文, 苗世洪, 范志华, 等. 不平衡电网电压下柔性直流输电系统功率滑模补偿策略[J]. 电工技术学报, 2018, 33(14): 3296-3305. LIU Z W, MIAO S H, FAN Z H, et al. Power sliding mode compensation strategy of VSC-HVDC under unbalanced grid voltage[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3296-3305(in Chinese).
[19]	SUH Y, LIPO T A. Modeling and analysis of instantaneous active and reactive power for PWM AC/DC converter under generalized unbalanced network[J]. IEEE Transactions on Power Delivery, 2006, 21(3): 1530-1540. doi: 10.1109/TPWRD.2005.860274
[20]	ZHANG Y C, QU C Q. Model predictive direct power control of PWM rectifiers under unbalanced network conditions[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4011-4022. doi: 10.1109/TIE.2014.2387796
[21]	梁营玉. 不对称电网电压下基于降阶矢量谐振器的MMC-HVDC直接功率控制策略[J]. 中国电机工程学报, 2017, 37(24): 7294-7303. LIANG Y Y. Direct power control strategy based on reduced order vector resonant controller for MMC-HVDC under unbalanced grid voltages[J]. Proceedings of the CSEE, 2017, 37(24): 7294-7303(in Chinese).
[22]	刘勇智, 鄯成龙, 林博闻, 等. 基于自适应二阶终端滑模的 SRM 直接转矩控制[J]. 北京亚洲成人在线一二三四五六区学报, 2018, 44(10): 2043-2051. LIU Y Z, SHAN C L, LIN B W, et al. Direct torque control of switched reluctance motor based on adaptive second-order terminal sliding mode[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(10): 2043-2051(in Chinese).
[23]	李慧洁, 蔡远利. 基于双幂次趋近律的滑模控制方法[J]. 控制与决策, 2016, 31(3): 498-502. LI H J, CAI Y L. Sliding mode control with double power reaching law[J]. Control and Decision, 2016, 31(3): 498-502(in Chinese).
[24]	高洁, 王华宇, 徐萌. 开关磁阻电机的分数阶终端滑模控制[J]. 电机与控制学报, 2022, 26(2): 142-150. GAO J, WANG H Y, XU M. Improved terminal sliding mode control strategy of switched reluctance motors based on fractional calculus[J]. Electric Machines and Control, 2022, 26(2): 142-150(in Chinese).
[25]	李逃昌. 基于新型趋近律的非线性积分滑模控制方法[J]. 控制工程, 2019, 26(11): 2031-2035. LI T C. Nonlinear integral sliding mode control method based on new reaching law[J]. Control Engineering of China, 2019, 26(11): 2031-2035(in Chinese).
[26]	刘金琨. 滑模变结构控制MATLAB仿真: 基本理论与设计方法[M]. 4版. 北京: 清华大学出版社, 2019: 38-39. LIU J K. Sliding mode control design and MATLAB simulation: the basic theory and design method[M]. 4th ed. Beijing: Tsinghua University Press, 2019: 38-39(in Chinese).
[27]	AKAGI H, KANAZAWA Y, NABAE A. Instantaneous reactive power compensators comprising switching devices without energy storage components[J]. IEEE Transactions on Industry Applications, 1984, 20(3): 625-630. doi: 10.1109/TIA.1984.4504460
[28]	杨锁昌, 张宽桥, 陈鹏. 带攻击角度约束的自适应终端滑模导引律[J]. 北京亚洲成人在线一二三四五六区学报, 2016, 42(8): 1566-1574. YANG S C, ZHANG K Q, CHEN P. Adaptive terminal sliding mode guidance law with impact angle constraint[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(8): 1566-1574(in Chinese).
[29]	潘菲, 朱宏玉. 航天器非奇异自适应终端滑模姿轨联合控制[J]. 北京亚洲成人在线一二三四五六区学报, 2020, 46(7): 1354-1362. PAN F, ZHU H Y. Spacecraft non-singular adaptive terminal sliding mode attitude-orbit coupling control[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(7): 1354-1362(in Chinese).
[30]	LU W X, OOI B T. Optimal acquisition and aggregation of offshore wind power by multiterminal voltage-source HVDC[J]. IEEE Transactions on Power Delivery, 2003, 18(1): 201-206. doi: 10.1109/TPWRD.2002.803826