基于时效网络的关键航空器识别方法

王红勇; 马丽书; 许平

doi:10.13700/j.bh.1001-5965.2023.0259

基于时效网络的关键航空器识别方法

doi: 10.13700/j.bh.1001-5965.2023.0259

中国民航大学空中交通管理学院，天津 300300

基金项目:

国家自然科学基金(U1833103)；天津市自然科学基金(21JCZDJC00840)

详细信息

通讯作者:
E-mail：hy_wang@cauc.edu.cn

中图分类号: V355
计量
- 文章访问数: 570
- HTML全文浏览量: 91
- PDF下载量: 17
- 被引次数: 0
出版历程
- 收稿日期: 2023-05-22
- 录用日期: 2023-09-09
- 网络出版日期: 2023-10-12
- 整期出版日期: 2025-05-31

Critical aircraft identification method based on temporal network

College of Air Traffic Management，Civil Aviation University of China，Tianjin 300300，China

Funds:

National Natural Science Foundation of China (U1833103); National Natural Science Foundation of Tianjin (21JCZDJC00840)

More Information

Corresponding author: E-mail：hy_wang@cauc.edu.cn

摘要

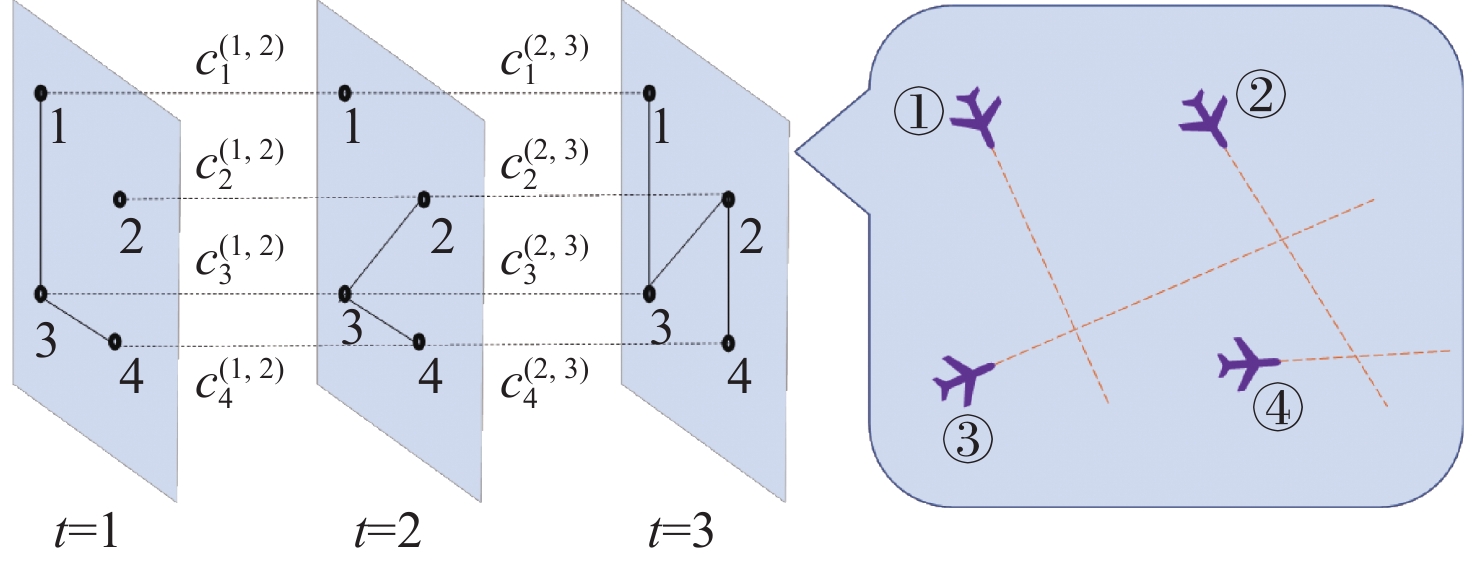
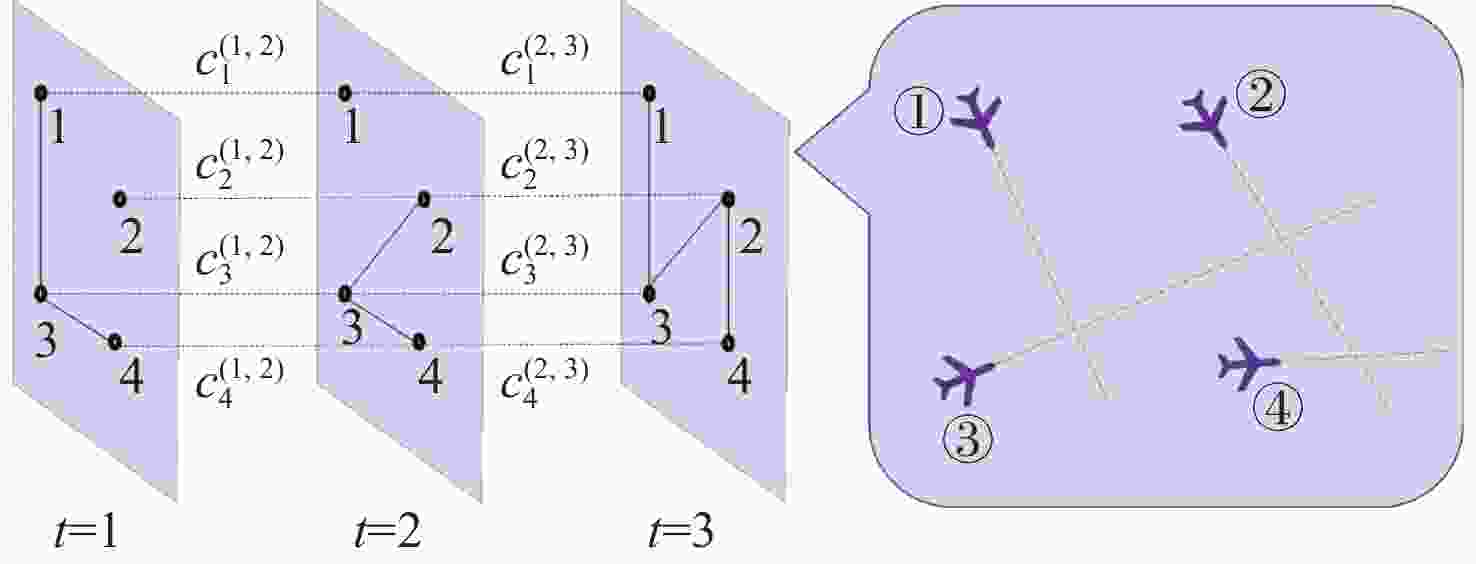
摘要:
针对空中交通态势中关键航空器识别问题，现有研究未能充分考虑空中交通实际运行中的时空效应。因此，提出一种基于时效网络的关键航空器识别方法。利用航空器间汇聚关系及其复杂性，通过邻居拓扑重叠系数构建时效网络模型，并基于特征向量中心性确定关键航空器。对关键航空器节点进行网络攻击观察扇区复杂性变化情况，并对比基于静态网络指标下的攻击，采用改进遗传算法为网络攻击删除的航空器节点分配新的进扇区时刻，从而验证关键航空器的选取效果。通过实际数据验证表明：所提方法相较于静态网络攻击在移除关键航空器时更高效地降低了扇区平均复杂性，改进的遗传算法求解关键航空器进扇区时刻分配问题时收敛性更高，使得扇区复杂性在一定时间段内更加平稳。分析关键航空器的控制效果表明：所提方法相较于静态网络更能准确地识别一段时间内对扇区复杂性影响较大的航空器。
- 航空运输 /
- 扇区复杂性 /
- 关键航空器 /
- 空中交通态势时效网络 /
- 网络攻击 /
- 遗传算法
Abstract:
In view of the problem of critical aircraft identification in air traffic situations, the existing research fails to fully consider the spatiotemporal effect in actual air traffic operation. Therefore, a method of critical aircraft identification based on a temporal network was proposed. Based on the convergence relationship between aircraft and its complexity, the temporal network model was constructed by the neighbor topological overlap coefficient, and the critical aircraft was determined based on the eigenvector centrality. Network attacks on critical aircraft nodes were carried out to observe the changes in sector complexity and compared with attacks based on static network indicators. The improved genetic algorithm was used to assign a new sector entry time to the aircraft node deleted by the network attack, so as to verify the selection effect of the critical aircraft. Actual data verification shows that compared with static network attacks, the proposed method can reduce the average sector complexity more efficiently when removing critical aircraft, and the improved genetic algorithm has higher convergence when solving the time allocation problem of critical aircraft entering the sector, making the sector complexity more stable in a certain period of time. The analysis of the control effect of critical aircraft shows that the temporal network method is more accurate than the static network in identifying the aircraft that has a greater influence on the sector complexity in a period of time.
- air transportation /
- sector complexity /
- critical aircraft /
- air traffic situation timeliness network /
- network attack /
- genetic algorithm

HTML全文

图 1 空中交通态势时效网络示意图

Figure 1. Temporal network of air traffic

下载: 全尺寸图片幻灯片

图 2 Class-1类设计准则等级函数

Figure 2. Class-1 design criteria level function

下载: 全尺寸图片幻灯片

图 3 扇区复杂性与航班数量

Figure 3. Sector complexity and number of flights

下载: 全尺寸图片幻灯片

图 4 网络攻击过程

Figure 4. Process of network attack

下载: 全尺寸图片幻灯片

图 5 扇区复杂性

Figure 5. Sector complexity

下载: 全尺寸图片幻灯片

图 6 扇区复杂性偏好函数曲线

Figure 6. Preference function curve of sector complexity

下载: 全尺寸图片幻灯片

图 7 航空器调整时间的偏好函数曲线

Figure 7. Preference function curve of aircraft adjustment time

下载: 全尺寸图片幻灯片

图 8 调整航空器比例偏好函数曲线

Figure 8. Preference function curve of aircraft proportion adjustemnt

下载: 全尺寸图片幻灯片

图 9 GA和GA2的计算结果

Figure 9. The calculation results of GA and GA2

下载: 全尺寸图片幻灯片

图 10 扇区复杂性对比

Figure 10. Sector complexity comparison

下载: 全尺寸图片幻灯片

图 11 扇区内汇聚关系数量

Figure 11. Number of convergence relationships within a sector

下载: 全尺寸图片幻灯片

图 12 航空器平均复杂性

Figure 12. Average complexity of aircraft

下载: 全尺寸图片幻灯片

图 13 航空器平均汇聚数量

Figure 13. Average convergence number of aircraft

下载: 全尺寸图片幻灯片

表 1 第7 min邻接矩阵

Table 1. Adjacency matrix at 7th minute

航空器	r_i1	r_i2	r_i3	r_i4	r_i5	r_i6	r_i7	r_i8
1	0	0	8.834	11.14	7.713	25.06	0	2.513
2	0	0	13.74	8.191	11.60	8.162	0	1.545
3	8.834	13.74	0	0	0	6.460	0.414	7.659
4	11.14	8.191	0	0	0	8.792	0	2.878
5	7.713	11.60	0	0	0	5.778	0.197	10.46
6	25.06	8.162	6.460	8.792	5.778	0	142.9	1.440
7	0	0	0.414	0	0.197	142.9	0	0
8	2.513	1.545	7.659	2.878	10.46	1.440	0	0

下载: 导出CSV

表 2 第33 min邻接矩阵

Table 2. Adjacency matrix at 33rd minute

航空器	r_i1	r_i2	r_i3	r_i4	r_i5	r_i6	r_i7	r_i8
1	0	4.167	3.349	34.05	100.6	153.1	0.512	0
2	4.167	0	7.662	3.413	0.636	3.776	7.864	45.34
3	3.349	7.662	0	0.529	0	3.332	4.724	12.29
4	34.05	3.413	0.529	0	0	36.84	79.08	0
5	100.6	0.636	0	0	0	90.44	0	0
6	153.1	3.776	3.332	36.84	90.44	0	12.49	0
7	0.512	7.864	4.724	79.08	0	12.49	0	0.254
8	0	45.34	12.29	0	0	0	0.254	0

下载: 导出CSV

表 3 GA2调整方案

Table 3. Adjusted scheme of GA2

航空器	原始进扇区时刻/min	时刻调整量/min
CQN2037	3	−1
CES5809	6	3
CES565	8	−1
CQH8954	10	−1
CSZ9880	15	−3
CXA8415	16	−1
CGH1003	29	2
CDG4871	37	−3
CGH1003	51	−2

下载: 导出CSV

参考文献(29)

[1]	SCHMIDT D K. On modeling ATC work load and sector capacity[J]. Journal of Aircraft, 1976, 13(7): 531-537. doi: 10.2514/3.44541
[2]	HURST M W, ROSE R M. Objective job difficulty, behavioural response, and sector characteristics in air route traffic control centres[J]. Ergonomics, 1978, 21(9): 697-708. doi: 10.1080/00140137808931772
[3]	NETJASOV F, JANIĆ M, TOŠIĆ V. Developing a generic metric of terminal airspace traffic complexity[J]. Transportmetrica, 2011, 7(5): 369-394. doi: 10.1080/18128602.2010.505590
[4]	KOPARDEKAR P, MAGYARITS S. Dynamic density: measuring and predicting sector complexity[C]//Proceedings of the 21st Digital Avionics Systems Conference. Piscataway: IEEE Press, 2002: 2C4.
[5]	LEE K, FERON E, PRITCHETT A. Describing airspace complexity: airspace response to disturbances[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(1): 210-222. doi: 10.2514/1.36308
[6]	LEE K, FERON E, PRITCHETT A. Air traffic complexity: an input-output approach[C]//Proceedings of the American Control Conference. Piscataway: IEEE Press, 2007: 474-479.
[7]	DELAHAYE D, ALLIOT J M, SCHOENAUER M, et al. Genetic algorithms for air traffic assignment[C]//Proceedings of the 11th European Conference on Artificial Intelligence. New York: ACM, 1994: 33-37.
[8]	DELAHAYE D, PUECHMOREL S. Air traffic complexity: towards an intrinsic metrics[C]//Proceedings of the 3rd USA/Europe Air Traffic Management R and D Seminar. Reston:AIAA,2000.
[9]	DELAHAYE D, PUECHMOREL S, HANSMAN J, et al. Air traffic complexity map based on non linear dynamical systems[J]. Air Traffic Control Quarterly, 2004, 12(4): 367-388. doi: 10.2514/atcq.12.4.367
[10]	张进, 胡明华, 张晨, 等. 空域复杂性建模[J]. 南京亚洲成人在线一二三四五六区学报, 2010, 42(4): 454-460. doi: 10.3969/j.issn.1005-2615.2010.04.011 ZHANG J, HU M H, ZHANG C, et al. Airspace complexity modeling[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(4): 454-460(in Chinese). doi: 10.3969/j.issn.1005-2615.2010.04.011
[11]	张进, 胡明华, 张晨. 空中交通管理中的复杂性研究[J]. 航空学报, 2009, 30(11): 2132-2142. doi: 10.3321/j.issn:1000-6893.2009.11.019 ZHANG J, HU M H, ZHANG C. Complexity research in air traffic management[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(11): 2132-2142(in Chinese). doi: 10.3321/j.issn:1000-6893.2009.11.019
[12]	徐肖豪, 黄宝军, 舒勤. 基于内禀属性的扇区复杂性评估[J]. 中国民航大学学报, 2013, 31(2): 22-28. doi: 10.3969/j.issn.1674-5590.2013.02.005 XU X H, HUANG B J, SHU Q. Sector complexity evaluation based on intrinsic attributes[J]. Journal of Civil Aviation University of China, 2013, 31(2): 22-28(in Chinese). doi: 10.3969/j.issn.1674-5590.2013.02.005
[13]	王红勇, 郭宇鹏. 基于航空器自主运行的空中交通复杂性建模[J]. 交通运输系统工程与信息, 2022, 22(2): 305-312. WANG H Y, GUO Y P. Air traffic complexity model based on aircraft self-separation operation[J]. Journal of Transportation Systems Engineering and Information Technology, 2022, 22(2): 305-312(in Chinese).
[14]	MORONE F, MAKSE H A. Influence maximization in complex networks through optimal percolation[J]. Nature, 2015, 524(7563): 65-68. doi: 10.1038/nature14604
[15]	陈诗, 任卓明, 刘闯, 等. 时序网络中关键节点的识别方法研究进展[J]. 电子科技大学学报, 2020, 49(2): 291-314. CHEN S, REN Z M, LIU C, et al. Identification methods of vital nodes on temporal networks[J]. Journal of University of Electronic Science and Technology of China, 2020, 49(2): 291-314(in Chinese).
[16]	WANG Z Q, PEI X B, WANG Y B, et al. Ranking the key nodes with temporal degree deviation centrality on complex networks[C]//Proceedings of the 29th Chinese Control and Decision Conference. Piscataway: IEEE Press, 2017: 1484-1489.
[17]	SCHOLTES I, WIDER N, GARAS A. Higher-order aggregate networks in the analysis of temporal networks: path structures and centralities[J]. The European Physical Journal B, 2016, 89(3): 61. doi: 10.1140/epjb/e2016-60663-0
[18]	ABBAS K, SHANG M S, ABBASI A, et al. Popularity and novelty dynamics in evolving networks[J]. Scientific Reports, 2018, 8(1): 6332. doi: 10.1038/s41598-018-24456-2
[19]	TAYLOR D, MYERS S A, CLAUSET A, et al. Eigenvector-based centrality measures for temporal networks[J]. Multiscale Modeling & Simulation, 2017, 15(1): 537-574.
[20]	CARLETTI T, BATTISTON F, CENCETTI G, et al. Random walks on hypergraphs[J]. Physical Review E, 2020, 101(2): 022308.
[21]	ROZENSHTEIN P, GIONIS A. Temporal PageRank[C]//Proceedings of the Machine Learning and Knowledge Discovery in Databases. Berlin: Springer, 2016: 674-689.
[22]	HUANG D W, YU Z G. Dynamic-Sensitive centrality of nodes in temporal networks[J]. Scientific Reports, 2017, 7: 41454. doi: 10.1038/srep41454
[23]	CAI Q, ALAM S, DUONG V N. A spatial–temporal network perspective for the propagation dynamics of air traffic delays[J]. Engineering, 2021, 7(4): 452-464. doi: 10.1016/j.eng.2020.05.027
[24]	黄洋, 汤俊, 老松杨. 基于复杂网络的无人机飞行冲突解脱算法[J]. 航空学报, 2018, 39(12): 322222. HUANG Y, TANG J, LAO S Y. UAV flight conflict resolution algorithm based on complex network[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(12): 322222(in Chinese).
[25]	刘飞, 余敏建, 李佳威, 等. 基于复杂网络理论的飞行冲突关键点识别[J]. 空军工程大学学报(自然科学版), 2019, 20(4): 19-25. LIU F, YU M J, LI J W, et al. An identification of flight conflict key nodes based on complex network theory[J]. Journal of Air Force Engineering University (Natural Science Edition), 2019, 20(4): 19-25(in Chinese).
[26]	吴明功, 王泽坤, 甘旭升, 等. 基于复杂网络理论的关键飞行冲突点识别[J]. 西北工业大学学报, 2020, 38(2): 279-287. doi: 10.1051/jnwpu/20203820279 WU M G, WANG Z K, GAN X S, et al. Identification of key flight conflict nodes based on complex network theory[J]. Journal of Northwestern Polytechnical University, 2020, 38(2): 279-287(in Chinese). doi: 10.1051/jnwpu/20203820279
[27]	王兴隆, 苗尚飞. 空域扇区网络结构特性分析及韧性评估[J]. 北京亚洲成人在线一二三四五六区学报, 2021, 47(5): 904-911. WANG X L, MIAO S F. Structural characteristics analysis and resilience assessment of airspace sector network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(5): 904-911(in Chinese).
[28]	TANG J, SCELLATO S, MUSOLESI M, et al. Small-world behavior in time-varying graphs[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2010, 81: 055101.
[29]	杨剑楠, 刘建国, 郭强. 基于层间相似性的时序网络节点重要性研究[J]. 物理学报, 2018, 67(4): 279-286. YANG J N, LIU J G, GUO Q. Node importance idenfication for temporal network based on inter-layer similarity[J]. Acta Physica Sinica, 2018, 67(4): 279-286(in Chinese).